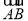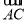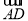Question

已知单调递增的等比数列{an}满足：

a2＋a3＋a4＝28，且a3＋2是a2和a4的等差中项．

(1)求数列{an}的通项公式an；

(2)令bn＝anlog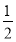an，Sn＝b1＋b2＋…＋bn，求使Sn＋n·2n＋1>50成立的最小的正整数n.

 

Answer 1

（1）2n（2）n＝5.

【解析】(1)设{an}的公比为q，由已知，得∴

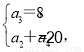
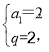即，解得或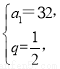 (舍去)∴an＝a1qn－1＝2n，

(2)bn＝2nlog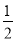2n＝－n·2n，

设Tn＝1×2＋2×22＋3×23＋…＋n×2n，①

则2Tn＝1×22＋2×23＋…＋(n－1)×2n＋n×2n＋1，②

①－②得－Tn＝(2＋22＋…＋2n)－n×2n＋1

＝－(n－1)·2n＋1－2，

∴Sn＝－Tn＝－(n－1)×2n＋1－2，

由Sn＋n·2n＋1>50，得

－(n－1)·2n＋1－2＋n·2n＋1>50，则2n>26，

故满足不等式的最小的正整数n＝5.