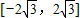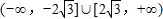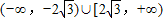题目内容
函数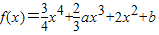 ,若f(x)仅在x=0处有极值,则a的取值范围是( )
,若f(x)仅在x=0处有极值,则a的取值范围是( )A.
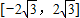
B.
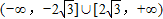
C.
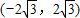
D.
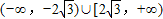
【答案】分析:求导函数,令导数为0,利用f(x)仅在x=0处有极值,可得△=4a2-48≤0,由此可求a的取值范围.
解答:解:求导函数,可得f′(x)=3x3+2ax2+4x
令f′(x)=3x3+2ax2+4x=0可得x=0或3x2+2ax+4=0,
∵f(x)仅在x=0处有极值,
∴△=4a2-48≤0,
∴-2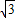 ≤a≤2
≤a≤2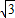
故选A.
点评:本题考查导数知识的运用,考查函数的极值,考查学生分析解决问题的能力,属于中档题.
解答:解:求导函数,可得f′(x)=3x3+2ax2+4x
令f′(x)=3x3+2ax2+4x=0可得x=0或3x2+2ax+4=0,
∵f(x)仅在x=0处有极值,
∴△=4a2-48≤0,
∴-2
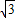 ≤a≤2
≤a≤2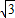
故选A.
点评:本题考查导数知识的运用,考查函数的极值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
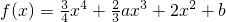 ,若f(x)仅在x=0处有极值,则a的取值范围是
,若f(x)仅在x=0处有极值,则a的取值范围是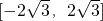
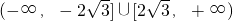
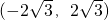
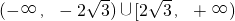
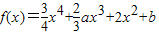 ,若f(x)仅在x=0处有极值,则a的取值范围是( )
,若f(x)仅在x=0处有极值,则a的取值范围是( )