题目内容
(本小题满分高☆考♂资♀源*网12分)
设椭圆![]() ,抛物线
,抛物线![]() 。
。
若![]() 经过
经过![]() 的两个焦点,求
的两个焦点,求![]() 的离心率;
的离心率;
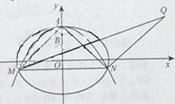
设A(0,b),![]() ,又M、N为
,又M、N为![]() 与
与![]() 不在y轴上的两个交点,若△AMN的垂心为
不在y轴上的两个交点,若△AMN的垂心为![]() ,且△QMN的重心在
,且△QMN的重心在![]() 上,求椭圆
上,求椭圆![]() 和抛物线
和抛物线![]() 的方程。
的方程。
【解析】考查椭圆和抛物线的定义、基本量,通过交点三角形来确认方程。
(1)由已知椭圆焦点(c,0)在抛物线上,可得:![]() ,由
,由
![]() 。
。
(2)由题设可知M、N关于y轴对称,设![]() ,由
,由![]() 的垂心为B,有
的垂心为B,有
![]() 。
。
由点![]() 在抛物线上,
在抛物线上,![]() ,解得:
,解得:![]()
故![]() ,得
,得![]() 重心坐标
重心坐标![]() .
.
由重心在抛物线上得:![]() ,
,![]() ,又因为M、N在椭圆上得:
,又因为M、N在椭圆上得:![]() ,椭圆方程为
,椭圆方程为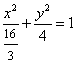 ,抛物线方程为
,抛物线方程为![]() 。
。

练习册系列答案
相关题目
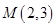 射到点
射到点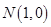 后被
后被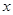 轴反射,求该光线及反射光线所在的直线方程。(请用直线的一般方程表示解题结果)[来源:高&考
轴反射,求该光线及反射光线所在的直线方程。(请用直线的一般方程表示解题结果)[来源:高&考