题目内容
已知函数f(x)=ax2-2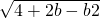 •x,g(x)=-
•x,g(x)=-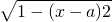 ,若存在x0,使得f(x0)是f(x)的最大值,g(x0)是g(x)的最小值,则这样的整数对(a,b)为________.
,若存在x0,使得f(x0)是f(x)的最大值,g(x0)是g(x)的最小值,则这样的整数对(a,b)为________.
(-1,-1)(-1,3)
分析:讨论a为0时不可能,要使f(x)有最大值,必须满足 ,求出此时的x=x0,根据g(x)取最小值时,x=x0=a,建立等量关系,结合a是整数,求出a和b的值.
,求出此时的x=x0,根据g(x)取最小值时,x=x0=a,建立等量关系,结合a是整数,求出a和b的值.
解答:若a=0, ,则f(x)无最大值,故a≠0,
,则f(x)无最大值,故a≠0,
∴f(x)为二次函数,
要使f(x)有最大值,必须满足 ,即a<0且
,即a<0且 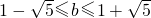 ,
,
此时, 时,f(x)有最大值.
时,f(x)有最大值.
又g(x)取最小值时,x=x0=a,
依题意,有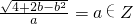 ,
,
则 ,
,
∵a<0且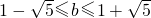 ,
,
∴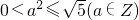 ,得a=-1,此时b=-1或b=3.
,得a=-1,此时b=-1或b=3.
∴满足条件的实数对(a,b)是(-1,-1),(-1,3).
故答案为:(-1,-1)(-1,3).
点评:本题主要考查了函数单调性的应用,以及函数的最值及其几何意义,属于基础题.
分析:讨论a为0时不可能,要使f(x)有最大值,必须满足
 ,求出此时的x=x0,根据g(x)取最小值时,x=x0=a,建立等量关系,结合a是整数,求出a和b的值.
,求出此时的x=x0,根据g(x)取最小值时,x=x0=a,建立等量关系,结合a是整数,求出a和b的值.解答:若a=0,
 ,则f(x)无最大值,故a≠0,
,则f(x)无最大值,故a≠0,∴f(x)为二次函数,
要使f(x)有最大值,必须满足
 ,即a<0且
,即a<0且 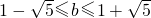 ,
,此时,
 时,f(x)有最大值.
时,f(x)有最大值.又g(x)取最小值时,x=x0=a,
依题意,有
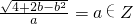 ,
,则
 ,
,∵a<0且
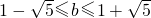 ,
,∴
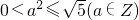 ,得a=-1,此时b=-1或b=3.
,得a=-1,此时b=-1或b=3.∴满足条件的实数对(a,b)是(-1,-1),(-1,3).
故答案为:(-1,-1)(-1,3).
点评:本题主要考查了函数单调性的应用,以及函数的最值及其几何意义,属于基础题.

练习册系列答案
相关题目