题目内容
设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
(1)q=-2.(2)见解析
1)解:设公比为q,则2a3=a5+a4,得2a1q2=a1q4+a1q3.又q≠0,a1≠0,q≠1,∴q=-2.
(2)证明:Sk+2+Sk+1-2Sk=(Sk+2-Sk)+(Sk+1-Sk)=ak+1+ak+2+ak+1=2ak+1+ak+1·(-2)=0,∴Sk+2,Sk,Sk+1成等差数列.
(2)证明:Sk+2+Sk+1-2Sk=(Sk+2-Sk)+(Sk+1-Sk)=ak+1+ak+2+ak+1=2ak+1+ak+1·(-2)=0,∴Sk+2,Sk,Sk+1成等差数列.

练习册系列答案
相关题目
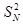 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.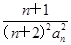 ,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<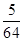 .
.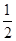 .
.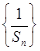 是等差数列;
是等差数列;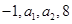 成等差数列,
成等差数列,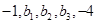 成等比数列,那么
成等比数列,那么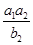 的值为( )
的值为( )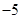
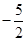
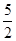
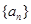 的前n项和为
的前n项和为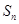 ,且
,且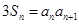 ,则
,则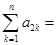 ( )
( )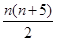
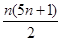
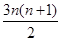

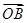 =a100·
=a100·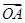 +a101
+a101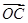 ,且A、B、C三点共线(该直线不过点O),则S200=________.
,且A、B、C三点共线(该直线不过点O),则S200=________.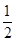 .
.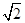 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.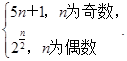
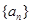 中,
中,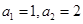 ,设
,设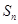 为数列
为数列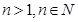 ,
,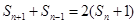 都成立,则
都成立,则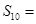 .
.