题目内容
已知二次函数f（x）满足f（1+x）=f（1-x），且f（0）=0，f（1）=1，若x∈[m，n]时f（x）的值域也为[m，n]，求m，n．
解：由f（1+x）=f（1-x）可知二次函数函数f（x）的对称轴为x=1，
又因f（0）=0，f（1）=1，则f（x）=-（x-1）2+1≤1，∴n≤1
∴f（x）在区间[m，n]上单调递增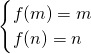
即 
，
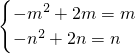而m＜n，所以m=0，n=1；
故答案为0，1．
分析：二次函数f（x）可以利用待定系数法求出函数解析式，注意到函数自身的最大值是1，能发现f（x）在区间[m，n]上单调递增，根据单调性建立等量关系．
点评：本题考查了函数解析式的求解，以及利用单调性求解函数的值域，属基础题．
又因f（0）=0，f（1）=1，则f（x）=-（x-1）2+1≤1，∴n≤1
∴f（x）在区间[m，n]上单调递增
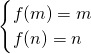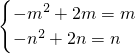即 ，而m＜n，所以m=0，n=1；
故答案为0，1．
分析：二次函数f（x）可以利用待定系数法求出函数解析式，注意到函数自身的最大值是1，能发现f（x）在区间[m，n]上单调递增，根据单调性建立等量关系．
点评：本题考查了函数解析式的求解，以及利用单调性求解函数的值域，属基础题．
练习册系列答案
阅读快车系列答案
相关题目