题目内容
已知{an}和{bn}都是公差不为零的等差数列,且
=2,则
等于( )
| lim |
| n→∞ |
| bn |
| an |
| lim |
| n→∞ |
| a1+a2+…+an |
| nb2n |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
分析:首先{an}和{bn}都是公差不为零的等差数列,可根据等差数列的性质列出等量关系式代入
=2,得到关系式,再求解.
| lim |
| n→∞ |
| bn |
| an |
解答:解:因为{an}和{bn}都是公差不为零的等差数列,
所以设bn=b1+(n-1)d1an=a1+(n-1)d2
故
=
=2,
又因为a1+a2+a3+…+an=na1+
和b2n=b1+(2n-1)d1代入
则
=
=
=
,
所以答案选C.
所以设bn=b1+(n-1)d1an=a1+(n-1)d2
故
| lim |
| n→∞ |
| bn |
| an |
| b1+(n-1)d1 |
| a1+(n-1)d2 |
又因为a1+a2+a3+…+an=na1+
| n(n+1)d2 |
| 2 |
则
| lim |
| n→∞ |
| a1+a2+…+an |
| nb2n |
na1+
| ||
| nb1+n(2n-1)d1 |
a1+
| ||
| b1+(2n-1)d1 |
| 1 |
| 8 |
所以答案选C.
点评:此题考查的是等差数列的性质,以及由性质关系在极限中的应用,计算量小但是有一定的技巧属于综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 等于
等于


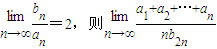 等于( )
等于( )

