题目内容
设![]()
(1)求![]() 的反函数
的反函数![]() ;
;
(2)讨论![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(3)令![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上的值域是
上的值域是![]() ,求
,求![]() 的取值范围。
的取值范围。
解:(1)![]()
(2)设![]() ,∵
,∵![]()
∴![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是减函数:
上是减函数:
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是增函数。7分
上是增函数。7分
(3)当![]() 时,∵
时,∵![]() 在
在![]() 上是减函数
上是减函数
∴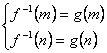 ,由
,由![]() 得
得![]() ,
,
即![]() ,
,
可知方程的两个根均大于![]() ,即
,即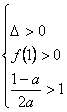
![]()
当![]() 时,∵
时,∵![]() 在
在![]() 上是增函数
上是增函数
∴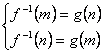
![]()
![]() (舍去)。
(舍去)。
综上,得 ![]() 。
。

练习册系列答案
相关题目
题目内容
设![]()
(1)求![]() 的反函数
的反函数![]() ;
;
(2)讨论![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(3)令![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上的值域是
上的值域是![]() ,求
,求![]() 的取值范围。
的取值范围。
解:(1)![]()
(2)设![]() ,∵
,∵![]()
∴![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是减函数:
上是减函数:
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是增函数。7分
上是增函数。7分
(3)当![]() 时,∵
时,∵![]() 在
在![]() 上是减函数
上是减函数
∴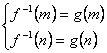 ,由
,由![]() 得
得![]() ,
,
即![]() ,
,
可知方程的两个根均大于![]() ,即
,即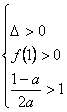
![]()
当![]() 时,∵
时,∵![]() 在
在![]() 上是增函数
上是增函数
∴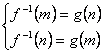
![]()
![]() (舍去)。
(舍去)。
综上,得 ![]() 。
。
