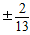题目内容
已知角α的终边在函数y=-
x的图象上,则1-2sinαcosα-3cos2α的值为( )
| 2 |
| 3 |
分析:通过角终边,求出角的正切值,利用同角三角函数基本关系把原式整理成
分子分母同时除以cos2α,把tanα的值代入即可求得答案.
| sin2α-2sinα•cosα-2cos2α |
| sin2α+cos2α |
解答:解:因为角α的终边在函数y=-
x的图象上,
所以tanα=-
,
1-2sinαcosα-3cos2α
=
=
=
=-
.
故选A.
| 2 |
| 3 |
所以tanα=-
| 2 |
| 3 |
1-2sinαcosα-3cos2α
=
| sin2α-2sinα•cosα-2cos2α |
| sin2α+cos2α |
=
| tan2α-2tanα-2 |
| tan2α+1 |
=
(-
| ||||
(-
|
=-
| 2 |
| 13 |
故选A.
点评:本题主要考查了三角函数的定义和同角三角函数的基本关系化简求值的问题.解题的过程中要巧妙利用三角函数关系中的平方关系.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
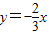 的图象上,则1-2sinαcosα-3cos2α的值为( )
的图象上,则1-2sinαcosα-3cos2α的值为( )