题目内容
设抛物线C:y2=2px,AB是过焦点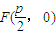 的弦,设A(x1,y1),B(x2,y2),O(0,0),l为准线,给出以下结论:
的弦,设A(x1,y1),B(x2,y2),O(0,0),l为准线,给出以下结论:①4x1x2=p2;②以AB为直径的圆与准线l相离;③
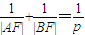 ; ④设准线l与x轴交于点N,则FN平分∠ANB;⑤过准线l上任一点M作抛物线的切线,则切点的连线必过焦点.则以上结论正确的是 将正确结论的序号填上去)
; ④设准线l与x轴交于点N,则FN平分∠ANB;⑤过准线l上任一点M作抛物线的切线,则切点的连线必过焦点.则以上结论正确的是 将正确结论的序号填上去)
【答案】分析:①由题意可设直线AB的方程为x=ky+ p,联立方程
p,联立方程 消去x可得y2-2pky-p2=0(*),根据方程的根与系数关系可求
消去x可得y2-2pky-p2=0(*),根据方程的根与系数关系可求
②分别过A,B作AP⊥l,BQ⊥l,垂足分别为P,Q,由抛物线的定义可知,AF=AP,BF=BQ,设AB的中点为C,过C作CD⊥l,垂足为D,则CD= =
=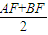
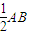 ,从而可判断
,从而可判断
③由定义可得AF=AP=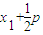 ,BF=BQ=
,BF=BQ=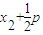 ,结合①中的方程的根与系数关系可求
,结合①中的方程的根与系数关系可求
④要证FN平分∠ANB,即∠ANF=∠BNF,根据题意只要证明KAN=-KBN,即可
⑤设出切线方程,联立直线与抛物线方程,根据方程的根与系数关系可求过切点的直线方程,进而可判断过 焦点
解答: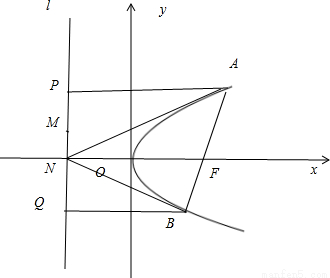 解:由题意可设直线AB的方程为x=ky+
解:由题意可设直线AB的方程为x=ky+ p
p
联立方程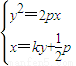 消去x可得y2-2pky-p2=0(*)
消去x可得y2-2pky-p2=0(*)
则 ,y1+y2=2pk,
,y1+y2=2pk,
∴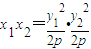 =
=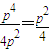
∴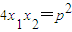 ①正确
①正确
分别过A,B作AP⊥l,BQ⊥l,垂足分别为P,Q
由抛物线的定义可知,AF=AP,BF=BQ
设AB的中点为C,过C作CD⊥l,垂足为D,则CD= =
= =
=
即所作圆的圆心C到准线的距离与圆的半径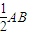 相等,则以AB为直径的圆与准线l相切,②错误
相等,则以AB为直径的圆与准线l相切,②错误
由于AF=AP=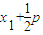 ,BF=BQ=
,BF=BQ=
由方程(*)可得,x1+x2=k(y1+y2)+p=2pk2+p
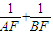 =
=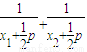 =
= =
=
=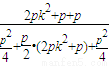 =
=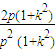 =
=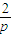 ③错误
③错误
由题意可知N(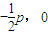 ),
),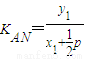 ,
,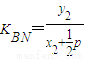
∴KAN+KBN=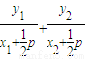 =
=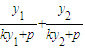
=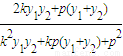 =
= =0
=0
∴KAN=-KBN,则可得∠ANF=∠BNF即FN平分∠ANB,④正确
设点M(-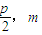 ),切点分别为E(x1,y1),F(x2,y2),从而可得切线的方程为y-m=k(x+
),切点分别为E(x1,y1),F(x2,y2),从而可得切线的方程为y-m=k(x+ )
)
联立方程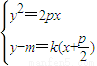 可得ky2-2py+kp2+2pm=0(*)
可得ky2-2py+kp2+2pm=0(*)
由题意可得,△=4p2-4k(kp2+2pm)=0即pk2+2mk-p=0
则k1k2=-1(k1,k2分别为切线ME,MF的斜率)
对应方程(*)可得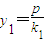 ,
,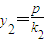
即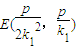 ,F
,F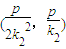
∴ =
=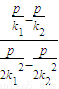 =
=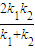 =-
=-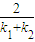
∴过切点EF的直线方程为y-
即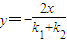
 =
= ,即直线EF过焦点(
,即直线EF过焦点(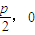 ),⑤正确
),⑤正确
点评:本题主要考查了抛物线的性质的应用,解题的关键是灵活利用抛物线的定义进行解题,属于综合性试题
 p,联立方程
p,联立方程 消去x可得y2-2pky-p2=0(*),根据方程的根与系数关系可求
消去x可得y2-2pky-p2=0(*),根据方程的根与系数关系可求②分别过A,B作AP⊥l,BQ⊥l,垂足分别为P,Q,由抛物线的定义可知,AF=AP,BF=BQ,设AB的中点为C,过C作CD⊥l,垂足为D,则CD=
 =
=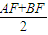
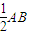 ,从而可判断
,从而可判断③由定义可得AF=AP=
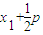 ,BF=BQ=
,BF=BQ=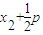 ,结合①中的方程的根与系数关系可求
,结合①中的方程的根与系数关系可求④要证FN平分∠ANB,即∠ANF=∠BNF,根据题意只要证明KAN=-KBN,即可
⑤设出切线方程,联立直线与抛物线方程,根据方程的根与系数关系可求过切点的直线方程,进而可判断过 焦点
解答:
 解:由题意可设直线AB的方程为x=ky+
解:由题意可设直线AB的方程为x=ky+ p
p联立方程
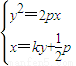 消去x可得y2-2pky-p2=0(*)
消去x可得y2-2pky-p2=0(*)则
 ,y1+y2=2pk,
,y1+y2=2pk,∴
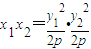 =
=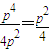
∴
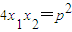 ①正确
①正确分别过A,B作AP⊥l,BQ⊥l,垂足分别为P,Q
由抛物线的定义可知,AF=AP,BF=BQ
设AB的中点为C,过C作CD⊥l,垂足为D,则CD=
 =
= =
=
即所作圆的圆心C到准线的距离与圆的半径
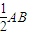 相等,则以AB为直径的圆与准线l相切,②错误
相等,则以AB为直径的圆与准线l相切,②错误由于AF=AP=
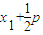 ,BF=BQ=
,BF=BQ=
由方程(*)可得,x1+x2=k(y1+y2)+p=2pk2+p
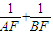 =
=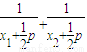 =
= =
=
=
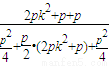 =
=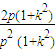 =
=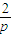 ③错误
③错误由题意可知N(
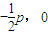 ),
),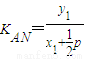 ,
,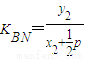
∴KAN+KBN=
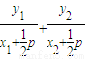 =
=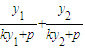
=
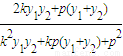 =
= =0
=0∴KAN=-KBN,则可得∠ANF=∠BNF即FN平分∠ANB,④正确
设点M(-
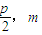 ),切点分别为E(x1,y1),F(x2,y2),从而可得切线的方程为y-m=k(x+
),切点分别为E(x1,y1),F(x2,y2),从而可得切线的方程为y-m=k(x+ )
)联立方程
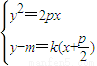 可得ky2-2py+kp2+2pm=0(*)
可得ky2-2py+kp2+2pm=0(*)由题意可得,△=4p2-4k(kp2+2pm)=0即pk2+2mk-p=0
则k1k2=-1(k1,k2分别为切线ME,MF的斜率)
对应方程(*)可得
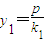 ,
,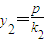
即
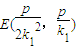 ,F
,F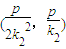
∴
 =
=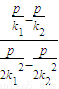 =
=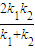 =-
=-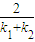
∴过切点EF的直线方程为y-

即
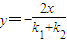
 =
= ,即直线EF过焦点(
,即直线EF过焦点(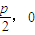 ),⑤正确
),⑤正确点评:本题主要考查了抛物线的性质的应用,解题的关键是灵活利用抛物线的定义进行解题,属于综合性试题

练习册系列答案
相关题目