题目内容
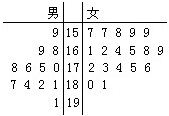
第26届世界大学生夏季运动会将于2011年8月12日至23日在深圳举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者,调查发现,这30名志愿者的身高如下:(单位:cm )
男 女
9 15 7 7 8 9 9
9 8 16 1 2 4 5 8 9
8 6 5 0 17 2 3 4 5 6
7 4 2 1 18 0 1
1 19
若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下定义为“非高个子”.
(1)如果用分层抽样的方法从志愿者中抽取5人,“高个子”和“非高个子”各抽取多少人?
(2)再从这5人中选2人,则至少有一人是“高个子”的概率是多少?
男 女
9 15 7 7 8 9 9
9 8 16 1 2 4 5 8 9
8 6 5 0 17 2 3 4 5 6
7 4 2 1 18 0 1
1 19
若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下定义为“非高个子”.
(1)如果用分层抽样的方法从志愿者中抽取5人,“高个子”和“非高个子”各抽取多少人?
(2)再从这5人中选2人,则至少有一人是“高个子”的概率是多少?
分析:(1)根据茎叶图,可得“高个子”12人,“非高个子”18人,每个人被抽中的概率是
,可得人数;
(2)搞清事件的对立关系:用事件A表示至少有一名“高个子”被选中,则它的对立事件
表示没有一名“高个子”被选中,通过求事件
的概率来求解.
| 1 |
| 6 |
(2)搞清事件的对立关系:用事件A表示至少有一名“高个子”被选中,则它的对立事件
. |
| A |
. |
| A |
解答:解:(1)根据茎叶图,有“高个子”12人,“非高个子”18人,
用分层抽样的方法,每个人被抽中的概率是
=
,
所以选中的“高个子”有12×
=2人,“非高个子”18×
=3人
(2)用事件A表示至少有一名“高个子”被选中,
则它的对立事件
表示没有一名“高个子”被选中,
则P(A)=1-
=1-
=
因此至少有一人是高个子的概率是
用分层抽样的方法,每个人被抽中的概率是
| 5 |
| 30 |
| 1 |
| 6 |
所以选中的“高个子”有12×
| 1 |
| 6 |
| 1 |
| 6 |
(2)用事件A表示至少有一名“高个子”被选中,
则它的对立事件
. |
| A |
则P(A)=1-
| ||
|
| 3 |
| 10 |
| 7 |
| 10 |
因此至少有一人是高个子的概率是
| 7 |
| 10 |
点评:本题为概率统计的综合,涉及茎叶图,分层抽样,和古典概型的求解,用对立事件的方式来求解往往会使问题简单,属基础题.

练习册系列答案
相关题目
 第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.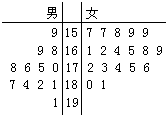 第26届世界大学生夏季运动会将于2011年8月12日到23日在中国广东举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.若从所有“高个子”
第26届世界大学生夏季运动会将于2011年8月12日到23日在中国广东举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.若从所有“高个子”
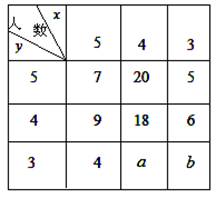
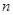 人,成绩只有
人,成绩只有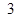 、
、 、
、 三种分值,设
三种分值,设 分别表示项目A与项目B成绩.例如:表中项目A成绩为
分别表示项目A与项目B成绩.例如:表中项目A成绩为 且
且 的概率是
的概率是 .
.
 名礼仪小姐,则
名礼仪小姐,则 的礼仪小姐中应抽多少人?
的礼仪小姐中应抽多少人? ,
, ,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.
,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.