题目内容
 如图,建立平面直角坐标系x0y,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.
如图,建立平面直角坐标系x0y,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
| 1 | 20 |
(1)求炮的最大射程;
(2)若规定炮弹的射程不小于6千米,设在此条件下炮弹射出的最大高度为f(k),求f(k)的最小值.
分析:(1)在y=kx-
(1+k2)x2(k>0)中,令y=0,求出x,利用基本不等式,即可求得炮的最大射程;
(2)利用配方法,求得炮弹射出的最大高度为f(k),根据炮弹的射程不小于6千米,确定k的范围,即可求f(k)的最小值.
| 1 |
| 20 |
(2)利用配方法,求得炮弹射出的最大高度为f(k),根据炮弹的射程不小于6千米,确定k的范围,即可求f(k)的最小值.
解答:解:(1)在y=kx-
(1+k2)x2(k>0)中,令y=0,得kx-
(1+k2)x2=0.-(2分)
由实际意义和题设条件知x>0,k>0.
∴x=
=
≤
=10,当且仅当k=1时取等号.-------------------(5分)
∴炮的最大射程是10千米.------------------------------------------------(6分)
(2)∵炮弹的射程不小于6千米,∴
≥6
∴
≤k≤3----------------------------------(8分)
y=kx-
(1+k2)x2=-
(1+k2)(x-
)2+
∴f(k)=
(
≤k≤3)-----------------------(10分)
∴f(k)=5(1-
)(
≤k≤3)--------(11分)
又f(k)在[
,3]上单调递增---------------(12分)
∴f(k)的最小值为
-----------------------------------------------(14分)
| 1 |
| 20 |
| 1 |
| 20 |
由实际意义和题设条件知x>0,k>0.
∴x=
| 20k |
| 1+k2 |
| 20 | ||
|
| 20 |
| 2 |
∴炮的最大射程是10千米.------------------------------------------------(6分)
(2)∵炮弹的射程不小于6千米,∴
| 20k |
| 1+k2 |
∴
| 1 |
| 3 |
y=kx-
| 1 |
| 20 |
| 1 |
| 20 |
| 10k |
| 1+k2 |
| 5k2 |
| (1+k2)2 |
∴f(k)=
| 5k2 |
| (1+k2)2 |
| 1 |
| 3 |
∴f(k)=5(1-
| 1 |
| 1+k2 |
| 1 |
| 3 |
又f(k)在[
| 1 |
| 3 |
∴f(k)的最小值为
| 1 |
| 2 |
点评:本题考查函数模型的运用,考查基本不等式,考查配方法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
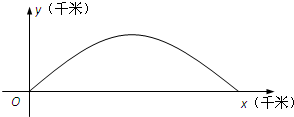 (2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
(2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
 ,
, 轴在地平面上,
轴在地平面上, 轴垂直于地
轴垂直于地 表示的曲线上,其中
表示的曲线上,其中 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标. 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
 ,
, 轴在地平面上,
轴在地平面上, 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程 表示的曲线上,其中
表示的曲线上,其中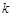 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标. 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.