题目内容
(A题)定义域为[-1,1]的奇函数y=f(x),若f(
)=-2,则f(-
)的值为( )
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据奇函数的定义,f(-x)=-f(x),将f(-
)转化为f(
),即可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵f(x)为定义在[-1,1]上的奇函数,
∴f(-x)=-f(x),
∴f(-
)=-f(
),
∵f(
)=-2,
∴f(-
)=2,
故选B.
∴f(-x)=-f(x),
∴f(-
| 1 |
| 2 |
| 1 |
| 2 |
∵f(
| 1 |
| 2 |
∴f(-
| 1 |
| 2 |
故选B.
点评:本题主要考查函数奇偶性定义的应用,对于函数的奇偶性的判断要先研究函数的定义域,然后再根据定义进行判断f(-x)与f(x)之间的关系.本题主要考查了应用奇偶性的定义求解函数的函数值,注意对f(-x)=-f(x)的应用.属于基础题.

练习册系列答案
相关题目
 的定义域为A,
的定义域为A,
 的定义域为B.
的定义域为B. ,求实数
,求实数 的取值范围.
的取值范围.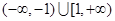 ,
,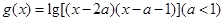 的定义域为集合B.
的定义域为集合B.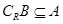 ,求实数
,求实数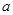 的范围。(R为实数集)
的范围。(R为实数集)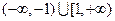 ,
,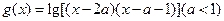 的定义域为集合B.
的定义域为集合B.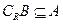 ,求实数
,求实数 的范围。(R为实数集)
的范围。(R为实数集)