题目内容
数列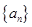 的前
的前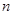 项和为
项和为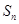 ,且
,且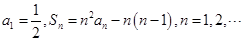
(1)写出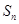 与
与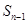 的递推关系式
的递推关系式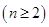 ,并求
,并求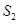 ,
,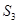 ,
,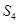 的值;
的值;
(2)猜想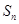 关于
关于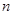 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
【答案】
(1)


(2)猜想 ,用数学归纳法证明:
,用数学归纳法证明:
【解析】
试题分析:(1)由
 得:
得: ,
,
即 ,
,  .
.
 可得
可得


(2)由(1)可猜想 ,下面用数学归纳法证明:
,下面用数学归纳法证明:
(i) 当 时,
时, ,猜想成立.
,猜想成立.
(ii)假设当 时,
时, 成立,
成立,
则当 时,
时,



故当 时,
时, ,猜想成立.
,猜想成立.
由(i)(ii)可得, 对一切正整数
对一切正整数 都成立.
都成立. 
 关于
关于 的表达式为
的表达式为 .
.
考点:本题主要考查归纳推理及数学归纳法。
点评:中档题,在高考命题中,单独考查数学归纳法已不多见,但”归纳、猜想、证明”的思想方法,确实是一种重要的方法,因此,应注意熟练掌握。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前
的前 项和为
项和为 ,数列
,数列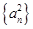 的前
的前 ,且
,且 .
. 对
对 恒成立,求
恒成立,求 的最小值;
的最小值; 成等差数列,求正整数
成等差数列,求正整数 的值.
的值. ,数列
,数列 的前
的前 项和为
项和为 ,点
,点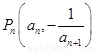 在曲线
在曲线 上
上 ,且
,且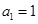 ,
, .
. 的前
的前 ,且满足
,且满足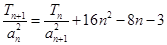 ,
, ,求数列
,求数列 ,
, .
. 的前
的前 项和为
项和为 ,且满足
,且满足
 ,在
,在 两项之间插入
两项之间插入 个数构成等差数列,求
个数构成等差数列,求 的值;
的值; ,并求
,并求 (用
(用 的前
的前 项和为
项和为 ,且
,且 ,则
,则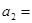 .
. ,点
,点
 在函数
在函数 的图象上,
的图象上, .
.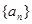 的通项公式;
的通项公式; 的前
的前 项和为
项和为 ,且满足
,且满足 ,求证:
,求证: 为等差数列;
为等差数列; 的值,使得数列
的值,使得数列