题目内容
(选修4-2矩阵与变换)已知在一个二阶矩阵M的变换作用下,点A(1,2)变成了点A′(4,5)点B(3,-1)变成了点B′(5,1).
(1)求矩阵M;
(2)若在矩阵M的变换作用下,点C(x,0)变成了点C′(4,y),求x,y.
(1)求矩阵M;
(2)若在矩阵M的变换作用下,点C(x,0)变成了点C′(4,y),求x,y.
分析:(1)利用待定系数法求解.先设所求的矩阵,再利用矩阵的乘法得到方程组,最后求解方程组即得.
(2)由于在矩阵M的变换作用下,点C(x,0)变成了点C′(4,y),利用(1)的结论,及矩阵相等的条件,可求x,y的值.
(2)由于在矩阵M的变换作用下,点C(x,0)变成了点C′(4,y),利用(1)的结论,及矩阵相等的条件,可求x,y的值.
解答:解(1)设该二阶矩阵为M=
,
由题意得
=
,
=
,
所以
,
解得 M=
.
(2)因为在矩阵M的变换作用下,点C(x,0)变成了点C′(4,y),
所以
=
=
,解得x=2,y=2.
|
由题意得
|
|
|
|
|
|
所以
|
解得 M=
|
(2)因为在矩阵M的变换作用下,点C(x,0)变成了点C′(4,y),
所以
|
|
|
|
点评:本题以变换为载体,主要考查了二阶矩阵的乘法,考查待定系数法,属于基础题.

练习册系列答案
相关题目
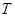 是将平面上每个点
是将平面上每个点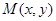 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点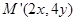 。
。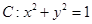 在变换
在变换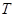 是将平面上每个点
是将平面上每个点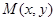 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点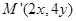 。
。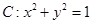 在变换
在变换