题目内容
若关于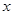 的不等式
的不等式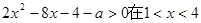 内有解,则实数
内有解,则实数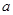 的取值范围是( )
的取值范围是( )
A. B.
B.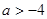 C.
C.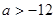 D.
D.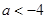
【答案】
D
【解析】
试题分析:关于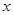 的不等式
的不等式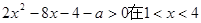 内有解,
内有解,
即:a<2x²-8x-4在1<x<4内有解,
令f(x)=2x²-8x-4=2(x-2)²-12
当x=2时f(x)取最小值f(2)=-12
当x=4时f(x)取最大值f(4)=2(4-2)²-12=-4
所以-12=<f(x)<-4
要使a<f(x)有解,则a不能大于也不能等于-4,否则a>=-4>f(x)
所以a的取值范围是a<-4,故选D。
考点:本题主要考查一元二次不等式解的讨论,二次函数的性质。
点评:中档题,此类问题的一般解法就是转化成而产生的最值问题,结合二次函数的图象和性质加以解决。

练习册系列答案
相关题目
若关于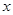 的不等式x2-3x-2-a >0在1<x<4内有解,则实数
的不等式x2-3x-2-a >0在1<x<4内有解,则实数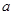 的取值范围是 ( )
的取值范围是 ( )
| A.a<-4 | B.a>-4 | C.a>2 | D.a<2 |
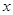 的不等式
的不等式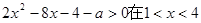 内有解,则实数
内有解,则实数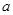 的取值范围是
的取值范围是 B.
B.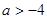 C.
C.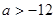 D.
D.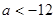
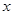 的不等式
的不等式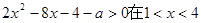 内有解,则实数
内有解,则实数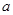 的取值范围是( )
的取值范围是( ) B.
B.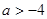
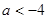 D.
D.