Question

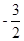设点F(0,),动圆P经过点F且和直线y=相切，记动圆的圆心P的轨迹为曲线W.

⑴求曲线W的方程；⑵过点F作相互垂直的直线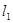，，分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值；②分别在A,B两点作曲线W的切线，这两条切线的交点记为Q,求证：QA⊥QB,且点Q在某一定直线上。

 

Answer 1

【答案】

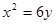（1）；（2）.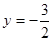

【解析】本试题主要是考查直线与圆的位置关系，以及抛物线方程的求解，和三角形面积的计算。

解：⑴由切线性质及抛物线定义知W的方程: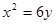

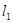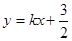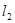⑵①设方程：，方程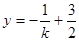：，由弦长公式易知：四边形ABCD的面积S==18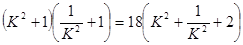≥72，K=±1时，.

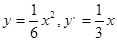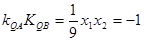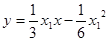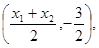②由⑴知W的方程为：，故，则：QA⊥QB.联立方程和得交点Q即Q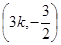，当k取任何非零实数时，点Q总在定直线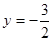上。