题目内容
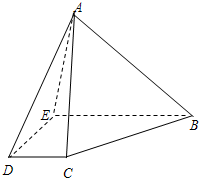 如图,在四棱锥A-BCDE中,底面BCDE是直角梯形,∠BED=90°,BE∥CD,AB=6,BC=5,
如图,在四棱锥A-BCDE中,底面BCDE是直角梯形,∠BED=90°,BE∥CD,AB=6,BC=5,| CD |
| BE |
| 1 |
| 3 |
(1)求证:平面ADE⊥平面ABE;
(2)过点D作面α∥平面ABC,分别于BE,AE交于点F,G,求△DFG的面积.
分析:(1)欲证平面ADE⊥平面ABE,根据面面垂直的判定定理可知在平面ABE内一直线与平面ADE垂直,根据面面垂直的性质可知DE⊥平面ABE,则AB⊥DE,而AB⊥AE,根据线面垂直的判定定理可知AB⊥平面ADE,满足面面垂直的判定定理所需条件;
(2)根据先证四边形BCDF为平行四边形,求出DF,根据比例关系求出FG,由(1)易证:FG⊥平面ADE,则FG⊥DG,从而求出DG,最后利用直角三角形的面积公式求出所求即可.
(2)根据先证四边形BCDF为平行四边形,求出DF,根据比例关系求出FG,由(1)易证:FG⊥平面ADE,则FG⊥DG,从而求出DG,最后利用直角三角形的面积公式求出所求即可.
解答: 证明:(1)因为侧面ABE⊥底面BCDE,
证明:(1)因为侧面ABE⊥底面BCDE,
侧面ABE∩底面BCDE=BE,
DE?底面BCDE,
DE⊥BE,
所以DE⊥平面ABE,
所以AB⊥DE,
又因为AB⊥AE,
所以AB⊥平面ADE,
所以平面ADE⊥平面ABE;7
(2)因为平面α∥平面ABC,
所以DF∥BC,同理FG∥AB9
所以四边形BCDF为平行四边形.
所以DF=BC=5,CD=BF,
因为
=
,所以
=
所以FG=
AB=411
由(1)易证:FG⊥平面ADE,
所以FG⊥DG,
所以DG=3
所以△DFG的面积S=6.14
 证明:(1)因为侧面ABE⊥底面BCDE,
证明:(1)因为侧面ABE⊥底面BCDE,侧面ABE∩底面BCDE=BE,
DE?底面BCDE,
DE⊥BE,
所以DE⊥平面ABE,
所以AB⊥DE,
又因为AB⊥AE,
所以AB⊥平面ADE,
所以平面ADE⊥平面ABE;7
(2)因为平面α∥平面ABC,
所以DF∥BC,同理FG∥AB9
所以四边形BCDF为平行四边形.
所以DF=BC=5,CD=BF,
因为
| CD |
| BE |
| 1 |
| 3 |
| EF |
| EB |
| 2 |
| 3 |
所以FG=
| 2 |
| 3 |
由(1)易证:FG⊥平面ADE,
所以FG⊥DG,
所以DG=3
所以△DFG的面积S=6.14
点评:本题主要考查平面与平面垂直的判定,以及线面垂直的性质和三角形的面积的计算,同时考查了空间想象能力,计算能力和推理能力,以及转化与划归的思想,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
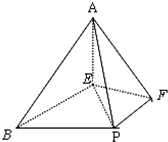 如图,在四棱锥A-BEFP中,AE⊥底面BEFP,BE⊥EF,
如图,在四棱锥A-BEFP中,AE⊥底面BEFP,BE⊥EF,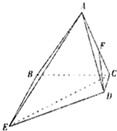 (2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC.
(2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC. =45
=45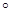 ,O是BC的中点,AO=
,O是BC的中点,AO= ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2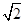 ,
,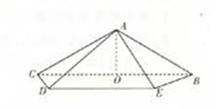
 ,AE=1,BE=FA=PB=2.
,AE=1,BE=FA=PB=2.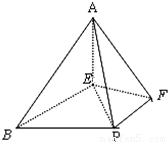
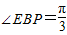 ,AE=1,BE=FA=PB=2.
,AE=1,BE=FA=PB=2.