题目内容
在△ABC中,已知 =1,
=1, =-2.
=-2.
(1)求AB边的长度;
(2)证明:tanA=2tanB;
(3)若| |=2,求|
|=2,求| |.
|.
解:(1)∵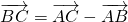
∴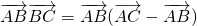 =
=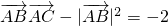
∵ =1
=1
∴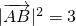 ,
,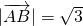 即AB边的长度为
即AB边的长度为 (3分)
(3分)
(2)由已知 =1,
=1, =-2.
=-2.
可得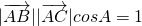 ①
①
 即
即 ②
②
由①②得,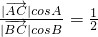
由正弦定理得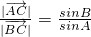
∴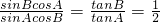
∴tanA=2tanB(8分)
(3)∵ ,由(2)中①得
,由(2)中①得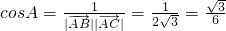
由余弦定理得 =
=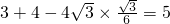 ∴
∴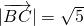 (12分)
(12分)
分析:(1)由已知可得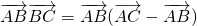 =
=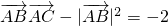 及
及 =1可求AB
=1可求AB
(2)由已知可得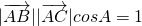 ,
, 结合正弦定理
结合正弦定理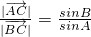 从而可得
从而可得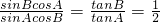 即证
即证
(3)由 ,及(2)可求
,及(2)可求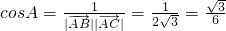
再由余弦定理得 =
=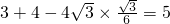 可求|
可求| |.
|.
点评:本题以向量的数量积为载体重在考查向量的基本运算,重点还运用了解三角形的正弦定理、余弦定理等解三角形的基本工具求解三角形的相关量,需要考试具备综合运用知识解决问题.
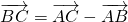
∴
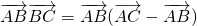 =
=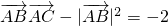
∵
 =1
=1∴
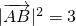 ,
,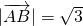 即AB边的长度为
即AB边的长度为 (3分)
(3分)(2)由已知
 =1,
=1, =-2.
=-2.可得
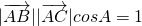 ①
① 即
即 ②
②由①②得,
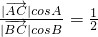
由正弦定理得
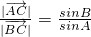
∴
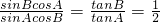
∴tanA=2tanB(8分)
(3)∵
 ,由(2)中①得
,由(2)中①得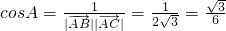
由余弦定理得
 =
=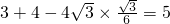 ∴
∴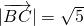 (12分)
(12分)分析:(1)由已知可得
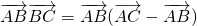 =
=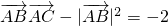 及
及 =1可求AB
=1可求AB(2)由已知可得
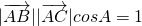 ,
, 结合正弦定理
结合正弦定理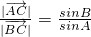 从而可得
从而可得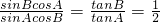 即证
即证(3)由
 ,及(2)可求
,及(2)可求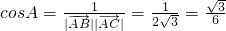
再由余弦定理得
 =
=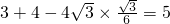 可求|
可求| |.
|.点评:本题以向量的数量积为载体重在考查向量的基本运算,重点还运用了解三角形的正弦定理、余弦定理等解三角形的基本工具求解三角形的相关量,需要考试具备综合运用知识解决问题.

练习册系列答案
相关题目