题目内容
设n是正整数,r为正有理数.(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:
 ;
;(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如
 .令
.令 的值.
的值.(参考数据:
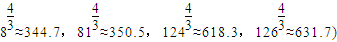 .
.
【答案】分析:(Ⅰ)先求出函数f(x)的导函数f′(x),令f'(x)=0,解得x=0,再求出函数的单调区间,进而求出最小值为f(0)=0;
(Ⅱ)根据(Ⅰ)知,即(1+x)r+1≥1+(r+1)x,令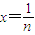 代入并化简得
代入并化简得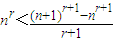 ,再令
,再令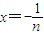 得,
得,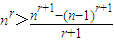 ,即结论得到证明;
,即结论得到证明;
(Ⅲ)根据(Ⅱ)的结论,令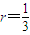 ,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得,
,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得,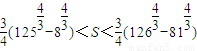 ,再由参考数据和条件进行求解.
,再由参考数据和条件进行求解.
解答:解;(Ⅰ)由题意得f'(x)=(r+1)(1+x)r-(r+1)=(r+1)[(1+x)r-1],
令f'(x)=0,解得x=0.
当-1<x<0时,f'(x)<0,∴f(x)在(-1,0)内是减函数;
当x>0时,f'(x)>0,∴f(x)在(0,+∞)内是增函数.
故函数f(x)在x=0处,取得最小值为f(0)=0.
(Ⅱ)由(Ⅰ),当x∈(-1,+∞)时,有f(x)≥f(0)=0,
即(1+x)r+1≥1+(r+1)x,且等号当且仅当x=0时成立,
故当x>-1且x≠0,有(1+x)r+1>1+(r+1)x,①
在①中,令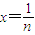 (这时x>-1且x≠0),得
(这时x>-1且x≠0),得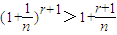 .
.
上式两边同乘nr+1,得(n+1)r+1>nr+1+nr(r+1),
即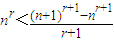 ,②
,②
当n>1时,在①中令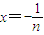 (这时x>-1且x≠0),
(这时x>-1且x≠0),
类似可得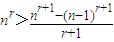 ,③
,③
且当n=1时,③也成立.
综合②,③得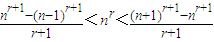 ,④
,④
(Ⅲ)在④中,令 ,n分别取值81,82,83,…,125,
,n分别取值81,82,83,…,125,
得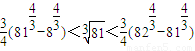 ,
,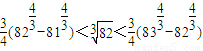 ,
,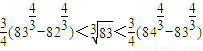 ,…
,…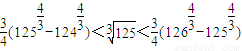 ,
,
将以上各式相加,并整理得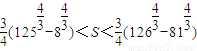 .
.
代入数据计算,可得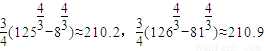
由[S]的定义,得[S]=211.
点评:本题考查了利用导数研究函数的单调性和求最值,以及学生的创新精神,是否会观察,会抽象概括,会用类比的方法得出其它结论,难度较大,注意利用上一问的结论.
(Ⅱ)根据(Ⅰ)知,即(1+x)r+1≥1+(r+1)x,令
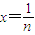 代入并化简得
代入并化简得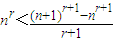 ,再令
,再令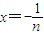 得,
得,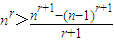 ,即结论得到证明;
,即结论得到证明;(Ⅲ)根据(Ⅱ)的结论,令
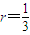 ,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得,
,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得,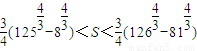 ,再由参考数据和条件进行求解.
,再由参考数据和条件进行求解.解答:解;(Ⅰ)由题意得f'(x)=(r+1)(1+x)r-(r+1)=(r+1)[(1+x)r-1],
令f'(x)=0,解得x=0.
当-1<x<0时,f'(x)<0,∴f(x)在(-1,0)内是减函数;
当x>0时,f'(x)>0,∴f(x)在(0,+∞)内是增函数.
故函数f(x)在x=0处,取得最小值为f(0)=0.
(Ⅱ)由(Ⅰ),当x∈(-1,+∞)时,有f(x)≥f(0)=0,
即(1+x)r+1≥1+(r+1)x,且等号当且仅当x=0时成立,
故当x>-1且x≠0,有(1+x)r+1>1+(r+1)x,①
在①中,令
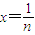 (这时x>-1且x≠0),得
(这时x>-1且x≠0),得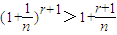 .
.上式两边同乘nr+1,得(n+1)r+1>nr+1+nr(r+1),
即
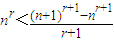 ,②
,②当n>1时,在①中令
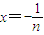 (这时x>-1且x≠0),
(这时x>-1且x≠0),类似可得
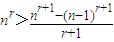 ,③
,③且当n=1时,③也成立.
综合②,③得
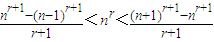 ,④
,④(Ⅲ)在④中,令
 ,n分别取值81,82,83,…,125,
,n分别取值81,82,83,…,125,得
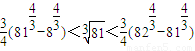 ,
,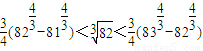 ,
,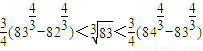 ,…
,…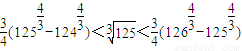 ,
,将以上各式相加,并整理得
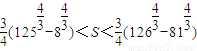 .
.代入数据计算,可得
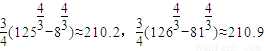
由[S]的定义,得[S]=211.
点评:本题考查了利用导数研究函数的单调性和求最值,以及学生的创新精神,是否会观察,会抽象概括,会用类比的方法得出其它结论,难度较大,注意利用上一问的结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目