题目内容
过双曲线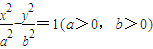 的右焦点F作双曲线在第一、第三象限的渐近线的垂线l,垂足为P,l与双曲线的左、右支的交点分别为A,B.
的右焦点F作双曲线在第一、第三象限的渐近线的垂线l,垂足为P,l与双曲线的左、右支的交点分别为A,B.(1)求证:P在双曲线的右准线上;
(2)求双曲线离心率的取值范围.
【答案】分析:(1)先设出双曲线半焦距,求得渐近线方程,则可求得过F的垂线方程,联立方程求得焦点p的横坐标,推断出在右准线上
(2)根据直线l与双曲线左右支均有交点,判断出该双曲线与其在第一、三象限的渐近线l1必交于第三象限.即l1的斜率必大于l的斜率,进而推断出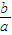 >
>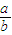 整理后即可求得a和c的不等式关系,求得离心率的范围.
整理后即可求得a和c的不等式关系,求得离心率的范围.
解答:解:(1)设双曲线半焦距为c,c>0,有F(c,0)
该渐近线方程为y=-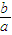 x,则过F的垂线为y=
x,则过F的垂线为y=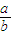 (x-c)
(x-c)
联立方程组可解得 x=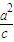 ,即在右准线x=
,即在右准线x=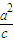 上.
上.
(2)因为直线l与双曲线左右支均有交点,则该双曲线与其在第一、三象限的渐近线l1必交于第三象限.
所以l1的斜率必大于l的斜率,即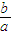 >
>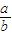 ,即b2 >a2,又b2=c2-a2,
,即b2 >a2,又b2=c2-a2,
所以c2>2a2
则离心率e=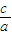 >
>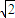
点评:本题主要考查了双曲线的简单性质.涉及了双曲线方程中a,b和c的关系,渐近线问题,离心率问题等.
(2)根据直线l与双曲线左右支均有交点,判断出该双曲线与其在第一、三象限的渐近线l1必交于第三象限.即l1的斜率必大于l的斜率,进而推断出
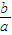 >
>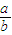 整理后即可求得a和c的不等式关系,求得离心率的范围.
整理后即可求得a和c的不等式关系,求得离心率的范围.解答:解:(1)设双曲线半焦距为c,c>0,有F(c,0)
该渐近线方程为y=-
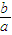 x,则过F的垂线为y=
x,则过F的垂线为y=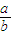 (x-c)
(x-c) 联立方程组可解得 x=
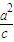 ,即在右准线x=
,即在右准线x=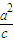 上.
上.(2)因为直线l与双曲线左右支均有交点,则该双曲线与其在第一、三象限的渐近线l1必交于第三象限.
所以l1的斜率必大于l的斜率,即
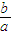 >
>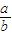 ,即b2 >a2,又b2=c2-a2,
,即b2 >a2,又b2=c2-a2,所以c2>2a2
则离心率e=
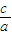 >
>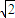
点评:本题主要考查了双曲线的简单性质.涉及了双曲线方程中a,b和c的关系,渐近线问题,离心率问题等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离
的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离 的右焦点F作圆
的右焦点F作圆 的切线FM(切点为M),交y轴于点P,若M为线段FP的中点, 则双曲线的离心率是
的切线FM(切点为M),交y轴于点P,若M为线段FP的中点, 则双曲线的离心率是 B.
B.
 C.2 D.
C.2 D.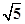
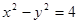 的右焦点F作倾斜角为
的右焦点F作倾斜角为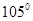 的直线,交双曲线于P、Q两点,
的直线,交双曲线于P、Q两点, |FQ|的值为__________.
|FQ|的值为__________.