题目内容
定义:项数为偶数的数列,若奇数项成等差数列,偶数项成等比数列,则称该数列为“对偶数列”.(1)若项数为20项的“对偶数列”{an},前4项为1,1,3,
 ,求该数列的通项公式及20项的和;
,求该数列的通项公式及20项的和;(2)设项数为2m(m∈N*)的“对偶数列”{an}前4项为1,1,3,
 ,试求该数列前n(1≤n≤2m,n∈N*)项的和Sn;
,试求该数列前n(1≤n≤2m,n∈N*)项的和Sn;(3)求证:等差数列{an}(an≠0)为“对偶数列”当且仅当数列{an}为非零常数数列.
【答案】分析:(1)由条件得,a1,a3,…,a19成等差数列,公差为2,a1=1;a2,a4,…,a20成等比数列,公比为 ,a2=1,由此能求出该数列的通项公式及20项的和;
,a2=1,由此能求出该数列的通项公式及20项的和;
(2)1≤n≤2m,n∈N*,当n为偶数时,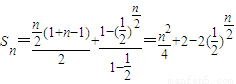 .当n为奇数时,
.当n为奇数时,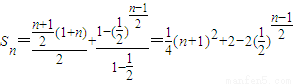 .
.
(3)设{an}为等差数列,公差为d.若{an}为“对偶数列”,则a2,a4,a6,…成等比数列,由此{an}为非零常数列.若{an}为非零常数列,则a1=a2=a3=a4=…,满足“对偶数列”的条件,因此{an}为“对偶数列”.
解答:解:(1)由条件得,a1,a3,…,a19成等差数列,公差为2,a1=1;a2,a4,…,a20成等比数列,公比为 ,a2=1.∴
,a2=1.∴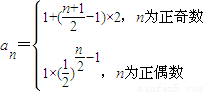
即
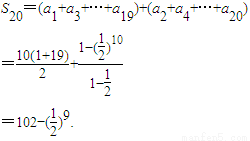
(2)1≤n≤2m,n∈N*,
当n为偶数时,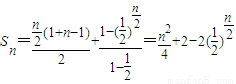 .
.
当n为奇数时,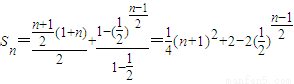 .
.
(3)设{an}为等差数列,公差为d.
若{an}为“对偶数列”,则a2,a4,a6,…成等比数列,∴a42=a2a6,(a1+3d)2=(a1+d)(a1+5d),得出d=0,
所以{an}为非零常数列.
若{an}为非零常数列,则a1=a2=a3=a4=…,满足“对偶数列”的条件,因此{an}为“对偶数列”.
点评:本题考查数列与函数的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
 ,a2=1,由此能求出该数列的通项公式及20项的和;
,a2=1,由此能求出该数列的通项公式及20项的和;(2)1≤n≤2m,n∈N*,当n为偶数时,
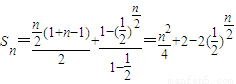 .当n为奇数时,
.当n为奇数时,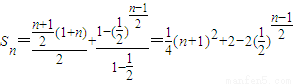 .
.(3)设{an}为等差数列,公差为d.若{an}为“对偶数列”,则a2,a4,a6,…成等比数列,由此{an}为非零常数列.若{an}为非零常数列,则a1=a2=a3=a4=…,满足“对偶数列”的条件,因此{an}为“对偶数列”.
解答:解:(1)由条件得,a1,a3,…,a19成等差数列,公差为2,a1=1;a2,a4,…,a20成等比数列,公比为
 ,a2=1.∴
,a2=1.∴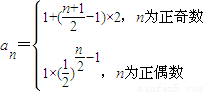
即

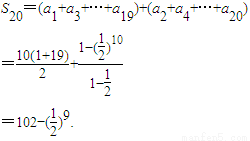
(2)1≤n≤2m,n∈N*,
当n为偶数时,
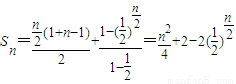 .
.当n为奇数时,
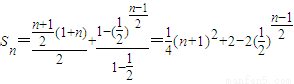 .
.(3)设{an}为等差数列,公差为d.
若{an}为“对偶数列”,则a2,a4,a6,…成等比数列,∴a42=a2a6,(a1+3d)2=(a1+d)(a1+5d),得出d=0,
所以{an}为非零常数列.
若{an}为非零常数列,则a1=a2=a3=a4=…,满足“对偶数列”的条件,因此{an}为“对偶数列”.
点评:本题考查数列与函数的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目