题目内容
设椭圆的中心在坐标原点,对称轴是坐标轴,一个顶点为A(0,2),右焦点F到点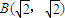 的距离为2.
的距离为2.(I)求椭圆的方程;
(Ⅱ)设经过点(0,-3)的直线l与椭圆相交于不同两点M,N满足
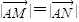 ,试求直线l的方程.
,试求直线l的方程.
【答案】分析:(Ⅰ)设出椭圆的标准方程,由右焦点F到点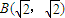 的距离为2列式求出c的值,结合b=2和求椭圆的标准方程;
的距离为2列式求出c的值,结合b=2和求椭圆的标准方程;
(Ⅱ)设出直线l的方程,和椭圆方程联立后利用根与系数关系求出两交点M、N的坐标和,从而求出线段MN的中点P的坐标,由 ,知点A在线段MN的垂直平分线上,由两点式写出AP的斜率,利用MN和AP垂直,斜率之积等于-1求直线l的斜率,则方程可求.
,知点A在线段MN的垂直平分线上,由两点式写出AP的斜率,利用MN和AP垂直,斜率之积等于-1求直线l的斜率,则方程可求.
解答:解:(Ⅰ) 依题意,设椭圆方程为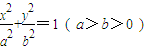 ,
,
则其右焦点坐标为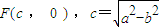 ,
,
由|FB|=2,得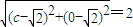 ,
,
即 ,故
,故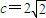 .
.
又∵b=2,∴a2=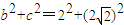 =12,
=12,
∴所求椭圆方程为 .
.
(Ⅱ)由题意可设直线l的方程为y=kx-3(k≠0),
由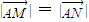 ,知点A在线段MN的垂直平分线上,
,知点A在线段MN的垂直平分线上,
由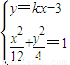 得x2+3(kx-3)2=12
得x2+3(kx-3)2=12
即(1+3k2)x2-18kx+15=0①
△=(-18k)2-4(1+3k2)×15=144k2-60>0
即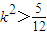 时方程①有两个不相等的实数根
时方程①有两个不相等的实数根
设M(x1,y1),N(x2,y2),线段MN的中点P(x,y)
则x1,x2是方程①的两个不等的实根,故有
从而有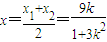 ,
,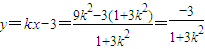
于是,可得线段MN的中点P的坐标为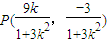
又由于k≠0,因此直线AP的斜率为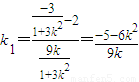
由AP⊥MN,得
即5+6k2=9,解得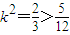 ,∴
,∴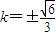 ,
,
∴所求直线l的方程为: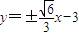 .
.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,运用了设而不求的解题思想,训练了两直线垂直的条件,是难题.
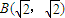 的距离为2列式求出c的值,结合b=2和求椭圆的标准方程;
的距离为2列式求出c的值,结合b=2和求椭圆的标准方程;(Ⅱ)设出直线l的方程,和椭圆方程联立后利用根与系数关系求出两交点M、N的坐标和,从而求出线段MN的中点P的坐标,由
 ,知点A在线段MN的垂直平分线上,由两点式写出AP的斜率,利用MN和AP垂直,斜率之积等于-1求直线l的斜率,则方程可求.
,知点A在线段MN的垂直平分线上,由两点式写出AP的斜率,利用MN和AP垂直,斜率之积等于-1求直线l的斜率,则方程可求.解答:解:(Ⅰ) 依题意,设椭圆方程为
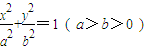 ,
,则其右焦点坐标为
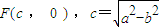 ,
,由|FB|=2,得
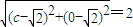 ,
,即
 ,故
,故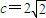 .
.又∵b=2,∴a2=
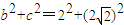 =12,
=12,∴所求椭圆方程为
 .
.(Ⅱ)由题意可设直线l的方程为y=kx-3(k≠0),
由
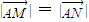 ,知点A在线段MN的垂直平分线上,
,知点A在线段MN的垂直平分线上,由
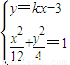 得x2+3(kx-3)2=12
得x2+3(kx-3)2=12即(1+3k2)x2-18kx+15=0①
△=(-18k)2-4(1+3k2)×15=144k2-60>0
即
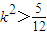 时方程①有两个不相等的实数根
时方程①有两个不相等的实数根设M(x1,y1),N(x2,y2),线段MN的中点P(x,y)
则x1,x2是方程①的两个不等的实根,故有

从而有
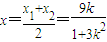 ,
,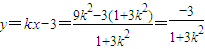
于是,可得线段MN的中点P的坐标为
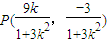
又由于k≠0,因此直线AP的斜率为
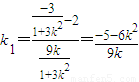
由AP⊥MN,得

即5+6k2=9,解得
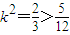 ,∴
,∴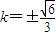 ,
,∴所求直线l的方程为:
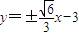 .
.点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,运用了设而不求的解题思想,训练了两直线垂直的条件,是难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
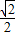 ,过椭圆外一点M(0,2)作直线l交椭圆与A,B两点,若△AOB的面积最大值为
,过椭圆外一点M(0,2)作直线l交椭圆与A,B两点,若△AOB的面积最大值为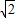 ,求此椭圆方程和直线l的方程.
,求此椭圆方程和直线l的方程.