Question

【题目】动点到直线的距离比它到点的距离大1．

(1)求点的轨迹的方程；

(2)过定点作直线,与(1)中的轨迹相交于、两点,为点关于原点的对称点,证明：；

(3)在(2)中，是否存在垂直于轴的直线被以为直径的圆截得的弦长恒为定值？若存在求出的方程；若不存在,请说明理由．

Answer 1

【答案】(1)；(2)证明见解析；(3)不存在,理由见解析.

【解析】

(1)根据题意结合抛物线的定义可以求出点的轨迹的方程；

(2)设出直线方程,与抛物线方程联立,得到一个一元二次方程,结合一元二次方程根与系数关系只要证明直线斜率之和为零即可；

(3)求出以为直径的圆的圆心和半径,利用垂径定理求出弦长,判断是不是定值即可.

(1)因为动点到直线的距离比它到点的距离大1,所以动点到直线的距离等于它到点的距离,由抛物线的定义可知：点的轨迹是以为焦点,原点为顶点的抛物线, 因此,所以点的轨迹的方程是

；

(2)由题意可设直线的方程为：与抛物线方程联立得：

,设、两点坐标为：

所以有.

由题意可知：,直线斜率分别记作：

所以有

,

所以；

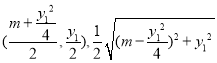(3) 以为直径的圆的圆心和半径分别为：,设直线的方程为,直线与以为直径的圆相交的弦长为,由圆的垂径定理可知：

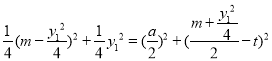,化简得：显然不是定值,故不存在直线被以为直径的圆截得的弦长恒为定值.