题目内容
与圆 相切,且在两坐标轴上截距相等的直线共有 条.
相切,且在两坐标轴上截距相等的直线共有 条.
 相切,且在两坐标轴上截距相等的直线共有 条.
相切,且在两坐标轴上截距相等的直线共有 条.4
本试题主要考查了直线与圆相切的情况,以及截距相等的分类讨论思想的运用。
当所求直线的方程的截距为0时,直线过原点,显然有两条直线满足题意;当截距不为0时,设所求直线的方程为:x+y=a(a≠0),由圆的方程得到:圆心坐标为(0,2),圆的半径为r=1,则圆心到直线的距离d=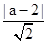 =r=1,即(a-2)2=2,,解得:a=2±
=r=1,即(a-2)2=2,,解得:a=2±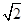 ,满足题意a的值有2个,所以满足题意的直线有2条.,综上,满足题意的直线有4条.,故答案为4.解决该试题的关键是对于截距是否为零讨论得到。
,满足题意a的值有2个,所以满足题意的直线有2条.,综上,满足题意的直线有4条.,故答案为4.解决该试题的关键是对于截距是否为零讨论得到。
当所求直线的方程的截距为0时,直线过原点,显然有两条直线满足题意;当截距不为0时,设所求直线的方程为:x+y=a(a≠0),由圆的方程得到:圆心坐标为(0,2),圆的半径为r=1,则圆心到直线的距离d=
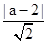 =r=1,即(a-2)2=2,,解得:a=2±
=r=1,即(a-2)2=2,,解得:a=2±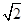 ,满足题意a的值有2个,所以满足题意的直线有2条.,综上,满足题意的直线有4条.,故答案为4.解决该试题的关键是对于截距是否为零讨论得到。
,满足题意a的值有2个,所以满足题意的直线有2条.,综上,满足题意的直线有4条.,故答案为4.解决该试题的关键是对于截距是否为零讨论得到。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
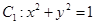 ,圆
,圆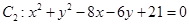 ,则两圆公切线的条数有( )
,则两圆公切线的条数有( ) 条
条 条
条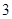 条
条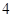 条
条 上的点到直线
上的点到直线 的最小距离是 .
的最小距离是 .  和圆外一点
和圆外一点 .
. 作圆的割线交圆于
作圆的割线交圆于 两点,若|
两点,若| |=4,求直线
|=4,求直线 ,求切线长及
,求切线长及 所在直线的方程.
所在直线的方程. 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,它的长轴长等于圆
,它的长轴长等于圆 的半径,则椭圆的标准方程是( )
的半径,则椭圆的标准方程是( )
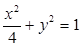


 ,
, 所连线段为直径的圆的方程是
所连线段为直径的圆的方程是  的圆心位于第三象限,则直线
的圆心位于第三象限,则直线 一定不经过第_______象限.
一定不经过第_______象限. 与圆
与圆 相交于
相交于 两点,且
两点,且 则
则 的值是( )
的值是( )


 与圆
与圆 的交点,且圆M的圆心到直线
的交点,且圆M的圆心到直线 的距离为
的距离为 ,求圆M的方程.
,求圆M的方程.