Question

（选修4-5  不等式证明选讲）
若不等式|x+1|+|

1

2

x-1|＜a的解集非空，求实数a的取值范围．

Answer 1

分析：令f（x）=|x+1|+|

1

2

x-1|，通过对x的范围的分类讨论去掉绝对值符号，转化为一次不等式，求得f（x）_min即可．

解答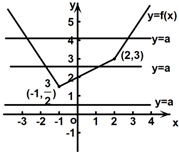：解：令f（x）=|x+1|+|

1

2

x-1|，
则f（x）=|x+1|+|

1

2

x-1|=

3 2 x，x≥2 1 2 x+2，-1≤x＜2 - 3 2 x，x＜-1

，．…（4分）
∴当x≥2时，f（x）=

3

2

x≥3；
当-1≤x＜2时，f（x）=

1

2

x+2∈[

3

2

，3）；
当x＜-1时，f（x）=-

3

2

x＞

3

2

．
∴f（x）_min=f（-1）=

3

2

．
又|x+1|+|

1

2

x-1|＜a非空，
∴a＞

3

2

．（7分）

点评：本题考查绝对值不等式的解法，通过对x的范围的分类讨论去掉绝对值符号是关键，考查构造函数与分类讨论思想，属于中档题．