题目内容
已知函数![]() ,点P1(x1,y1),P2(x2,y2)是函数f(x)图像上的两个点,且线段P1P2的中点P的横坐标为
,点P1(x1,y1),P2(x2,y2)是函数f(x)图像上的两个点,且线段P1P2的中点P的横坐标为![]() .
.
(1)求证:点P的纵坐标是定值;
(2)若数列{an}的通项公式为![]() ,求数列{an}的前m项的和Sm;
,求数列{an}的前m项的和Sm;
(3)若m∈N时,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
答案:
解析:
解析:
|
解:(1)由题可知: 点 (2)由⑴可知:对任意自然数 由于 所以, (2)∵ ∴ 依题意,①式应对任意 显然 记 ∴ |

练习册系列答案
相关题目
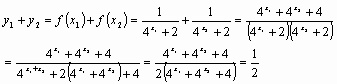
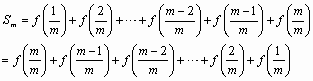
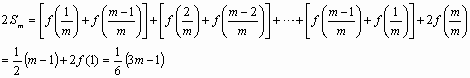 所以,
所以,