题目内容
为了对某课题进行研究，用分层抽样方法从三所科研单位A、B、C的相关人员中，抽取若干人组成研究小组，有关数据见下表（单位：人）：
(Ⅰ)确定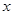
与
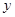的值；
(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言，求这2人都来自科研单位A的概率.
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | |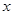
| B | 12 | 3 |
| C | 8 | |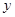
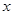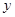与的值；(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言，求这2人都来自科研单位A的概率.
(Ⅰ)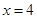
，
；
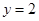(Ⅱ)选中的2人都来自科研单位A的概率为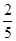
．
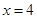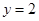，；(Ⅱ)选中的2人都来自科研单位A的概率为
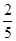．试题分析：(Ⅰ)确定
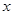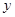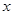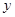与的值，由分层抽样的特点，是按比例抽样，首先计算出各层抽样比，由Ｂ中１２人抽出３人，故抽样比４：１，可根据抽样比计算出与的值；(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言，求这2人都来自科研单位A的概率，由(Ⅰ)可知，从科研单位A中抽取４人，从科研单位C中抽取２人，从这６人中选2人作专题发言，求这2人都来自科研单位A的概率，显然符合古典概率的特点，首先计算出从这６人中选2人作专题发言的基本事件数，再计算出这2人都来自科研单位A的基本事件数，由古典概率的求法可求得．试题解析：(Ⅰ)依题意得，
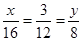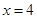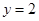，解得，. 5分(Ⅱ)记从科研单位A抽取的4人为
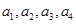，从科研单位C抽取的2人为
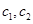，则从科研单位A、C抽取的6人中选2人作专题发言的基本事件有：
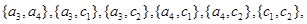共15种. 8分记“选中的2人都来自科研单位A”为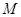事件
，则事件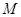包含的基本事件有：
共6种. 11分则
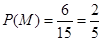.所以选中的2人都来自科研单位A的概率为 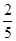12分
练习册系列答案
相关题目
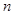个同学进行调查，结果显示这些同学的支出都在
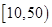（单位：元），其中支出在
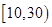（单位：元）的同学有
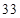人，其频率分布直方图如下图所示，则支出在
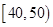（单位：元）的同学人数是（ ）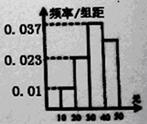
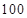
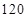
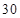
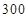
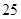人，美术特长生
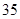人，音乐特长生
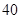人.用分层抽样的方法从中抽取
、
、
、
、
、
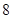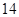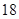
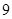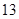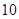