题目内容
（08年银川一中二模理）（12分）
已知
=（0，-2），
=（0，2）其中O为坐标原点。直线L: y=-2,动点P到直线L的距离为d,且d=|
|.
(1) 求动点P的轨迹方程；
(2) 直线m: y=
x+1(k>0)与点P的轨迹交于M，N两点，当
时，求直线m的倾斜角α的范围
(3) 设直线h与点P的轨迹交于C，D两点，若
=-12，那么直线h一定过B点吗？请说明理由。
解析：(1)由题意知，动点P到直线L距离与到定点B的距离相等。所以P的轨迹是以B为焦点，L为准线的抛物线，其轨迹方程为x2=8y
(2)由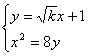
消去y得 x2-8
x-8=0, 设M(x1,y1), N(x2,y2) 
=64k+32>0, k>-
, x1+x2=8, x1x2=-8, y1+y2=x1+1+x2+1=8k+2, y1y2=(x1+1)( x2+1)=1, 
=x1x2+y1y2+2(y1+y2)+4=16k+1≥17, k≥1
tana≥1 且0≤a<1800 所以
≤a
所以的倾斜角为{a|≤a}
(3)设h:y=nx+b, 代入x2=8y中，得x2-8nx-8b=0. 设C(x3,y3). D(x4.y4). x3+x4=8n, x3+x4=-8b. 
x3x4+y3y4=b2-8b=-12, 得b=2或b=6.此时直线过点（0，2）或（0，6），故直线不一定过B点
练习册系列答案
相关题目
)ea x (a>0，a∈R))
≥0对x∈(0,+∞)恒成立，求a的取值范围
，（θ为参数）.表示的曲线为C，
．