题目内容
已知椭圆![]() 的一条准线方程是
的一条准线方程是![]() ,其左、右顶点分别是A、B;双曲线
,其左、右顶点分别是A、B;双曲线![]() 的一条渐近线方程为
的一条渐近线方程为![]() .
.
(1)求椭圆![]() 的方程及双曲线
的方程及双曲线![]() 的离心率;
的离心率;
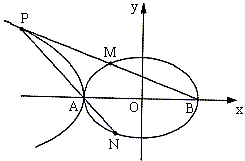
(2)在第二象限内取双曲线![]() 上一点P,连结BP交椭圆
上一点P,连结BP交椭圆![]() 于点M,连结PA并延长交椭圆
于点M,连结PA并延长交椭圆![]() 于点N,若
于点N,若![]() .求证:
.求证:![]() .
.
答案:
解析:
解析:
|
解:(1)由已知 ∴椭圆的方程为 又 ∴双曲线的离心率 (2)由(I) 设 ∴P点坐标为 将M、P坐标代入
消去 解之得: 由此可得: 当P为 即: 代入
MN⊥x轴,即 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,解之得:
,解之得:

 的一条准线方程是
的一条准线方程是 ,其左、右顶点分别是A、B;双曲线
,其左、右顶点分别是A、B;双曲线 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0. .求
.求 的值.
的值.
 的一条准线方程是
的一条准线方程是 ,其左、右顶点分别是A、B;双曲线
,其左、右顶点分别是A、B;双曲线 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0. .求
.求 的值.
的值.
 的一条准线方程是x=4,那么此椭圆的离心率是 .
的一条准线方程是x=4,那么此椭圆的离心率是 .