题目内容
已知函数 ;
;
(1)若不等式f(x)+2x+2<m在[0,2]内有解,求实数m的取值范围;
(2)若函数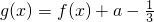 在区间[0,5]上没有零点,求实数a的取值范围.
在区间[0,5]上没有零点,求实数a的取值范围.
解:(1)∵ =
=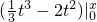 =
=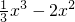
∴f′(x)=x2-4x
不等式f(x)+2x+2<m可化为m>x2-2x+2
∵不等式f(x)+2x+2<m在[0,2]内有解,
∴m>(x2-2x+2)min(x∈[0,2])
∵x2-2x+2=(x-1)2+1,
∴当x∈[0,2]时,(x2-2x+2)min=1
∴m>1,
∴实数m的取值范围为(1,+∞)
(2)由(1)得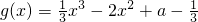 ,
,
∴g′(x)=x2-4x=x(x-4)
则当x∈[0,4]时,g′(x)≤0;当x∈(4,5]时,g′(x)>0
∴当x=4时,g(x)的最小值为g(4)=a-11
∵函数g(x)在区间[0,5]上没有零点,
∴a-11>0或
∴a>11,或a
∴实数a的取值范围为(11,+∞)∪(-∞, ).
).
分析:(1)根据定积分先求出函数的解析式,再利用分离参数法,将不等式f(x)+2x+2<m在[0,2]内有解,转化为m>(x2-2x+2)min(x∈[0,2]),即可求得实数m的取值范围;
(2)求导函数,确定g(x)的最小值,要使函数g(x)在区间[0,5]上没有零点,则a-11>0或 ,由此可求实数a的取值范围.
,由此可求实数a的取值范围.
点评:本题考查定积分,考查导数知识的运用,考查函数的零点,考查不等式有解问题,解题的关键是利用分离参数法,将不等式f(x)+2x+2<m在[0,2]内有解,转化为m>(x2-2x+2)min(x∈[0,2]).
 =
=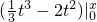 =
=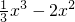
∴f′(x)=x2-4x
不等式f(x)+2x+2<m可化为m>x2-2x+2
∵不等式f(x)+2x+2<m在[0,2]内有解,
∴m>(x2-2x+2)min(x∈[0,2])
∵x2-2x+2=(x-1)2+1,
∴当x∈[0,2]时,(x2-2x+2)min=1
∴m>1,
∴实数m的取值范围为(1,+∞)
(2)由(1)得
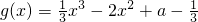 ,
,∴g′(x)=x2-4x=x(x-4)
则当x∈[0,4]时,g′(x)≤0;当x∈(4,5]时,g′(x)>0
∴当x=4时,g(x)的最小值为g(4)=a-11
∵函数g(x)在区间[0,5]上没有零点,
∴a-11>0或

∴a>11,或a

∴实数a的取值范围为(11,+∞)∪(-∞,
 ).
).分析:(1)根据定积分先求出函数的解析式,再利用分离参数法,将不等式f(x)+2x+2<m在[0,2]内有解,转化为m>(x2-2x+2)min(x∈[0,2]),即可求得实数m的取值范围;
(2)求导函数,确定g(x)的最小值,要使函数g(x)在区间[0,5]上没有零点,则a-11>0或
 ,由此可求实数a的取值范围.
,由此可求实数a的取值范围.点评:本题考查定积分,考查导数知识的运用,考查函数的零点,考查不等式有解问题,解题的关键是利用分离参数法,将不等式f(x)+2x+2<m在[0,2]内有解,转化为m>(x2-2x+2)min(x∈[0,2]).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. .
.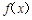 在(
在(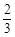 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;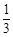 ,
, )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由. .
. 图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得图象向右平移
图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得图象向右平移 ,得到函数
,得到函数 的图象,写出
的图象,写出 的函数解析式;
的函数解析式; 且
且 与
与 共线,求
共线,求 的值.
的值. ,
, 
 在
在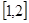 上是减函数,求实数
上是减函数,求实数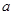 的取值范围;
的取值范围;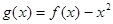 ,是否存在实数
,是否存在实数
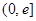 (
(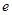 是自然常数)时,函数
是自然常数)时,函数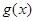 的最小值是3,若存在,求出
的最小值是3,若存在,求出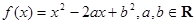 .
.
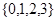 中任取一个元素
中任取一个元素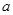 ,从集合
,从集合 中任取一个元素
中任取一个元素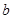 ,求方程
,求方程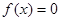 有两个不相等实根的概率;
有两个不相等实根的概率;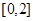 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程