题目内容
过抛物线y2=4x的焦点F作直线m交抛物线于点A、B,则△AOB是
- A.直角三角形
- B.锐角三角形
- C.钝角三角形
- D.不确定
C
分析:①当直线l不垂直于x轴时,设方程为y=k(x-1),联立不平为线方程可得k2x2-x(2k2+4)+k2=0.即可利用韦达定理得到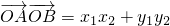 =(1+k2)x1x2-k2(x1+x2)+k2,
=(1+k2)x1x2-k2(x1+x2)+k2,
所以 =-3<0.②可得
=-3<0.②可得 =-3<0.由以上即可得到答案.
=-3<0.由以上即可得到答案.
解答:①抛物线的焦点坐标为(1,0),当直线l不垂直于x轴时,设方程为y=k(x-1),代入y2=4x,
得k2x2-x(2k2+4)+k2=0.
设点A、B的坐标分别为(x1,y1),(x2,y2),
根据韦达定理,有x1+x2=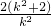 ,x1x2=1.
,x1x2=1.
因为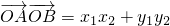 =(1+k2)x1x2-k2(x1+x2)+k2,
=(1+k2)x1x2-k2(x1+x2)+k2,
所以 =-3<0,
=-3<0,
所以∠AOB为钝角,则△AOB是钝角三角形.
②当斜率不存在时,A(1,2),B(1,-2),所以可得 =-3<0,
=-3<0,
所以∠AOB为钝角,则△AOB是钝角三角形.
故选C.
点评:本题主要考查了抛物线的方程与性质,在涉及直线与圆锥曲线问题时,设直线方程的时候一定要考虑到斜率不存在的情况;并且解决此类问题的方法一般是联立直线与圆锥曲线的方程借助于韦达定理解决问题,此类题目属于中档题型.
分析:①当直线l不垂直于x轴时,设方程为y=k(x-1),联立不平为线方程可得k2x2-x(2k2+4)+k2=0.即可利用韦达定理得到
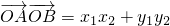 =(1+k2)x1x2-k2(x1+x2)+k2,
=(1+k2)x1x2-k2(x1+x2)+k2,所以
 =-3<0.②可得
=-3<0.②可得 =-3<0.由以上即可得到答案.
=-3<0.由以上即可得到答案.解答:①抛物线的焦点坐标为(1,0),当直线l不垂直于x轴时,设方程为y=k(x-1),代入y2=4x,
得k2x2-x(2k2+4)+k2=0.
设点A、B的坐标分别为(x1,y1),(x2,y2),
根据韦达定理,有x1+x2=
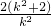 ,x1x2=1.
,x1x2=1.因为
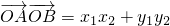 =(1+k2)x1x2-k2(x1+x2)+k2,
=(1+k2)x1x2-k2(x1+x2)+k2,所以
 =-3<0,
=-3<0,所以∠AOB为钝角,则△AOB是钝角三角形.
②当斜率不存在时,A(1,2),B(1,-2),所以可得
 =-3<0,
=-3<0,所以∠AOB为钝角,则△AOB是钝角三角形.
故选C.
点评:本题主要考查了抛物线的方程与性质,在涉及直线与圆锥曲线问题时,设直线方程的时候一定要考虑到斜率不存在的情况;并且解决此类问题的方法一般是联立直线与圆锥曲线的方程借助于韦达定理解决问题,此类题目属于中档题型.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A,B两点,则|AB|=( )
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为( )
| A、5 | ||
B、
| ||
C、
| ||
D、
|