题目内容
如图,在三棱柱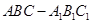 中,
中,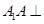 平面
平面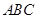 ,
,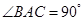 ,
,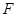 为棱
为棱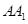 上的动点,
上的动点,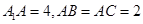 .
.
⑴当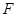 为
为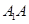 的中点,求直线
的中点,求直线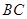 与平面
与平面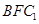 所成角的正弦值;
所成角的正弦值;
⑵当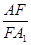 的值为多少时,二面角
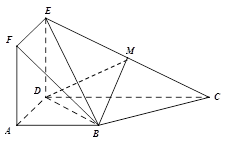
的值为多少时,二面角 的大小是45
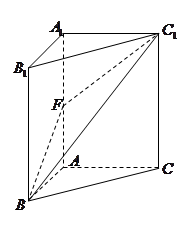
的大小是45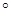 .
.
(1)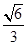 ,(2)
,(2)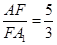 .
.
解析试题分析:(1)此小题考查用空间向量解决线面角问题,只需找到面的法向量与线的方向向量,注意用好如下公式: ,且线面角的范围为:
,且线面角的范围为: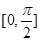 ;(2)此小题考查的是用空间向量解决面面角问题,只需找到两个面的法向量,但由于
;(2)此小题考查的是用空间向量解决面面角问题,只需找到两个面的法向量,但由于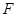 点坐标未知,可先设出,利用二面角
点坐标未知,可先设出,利用二面角 的大小是45
的大小是45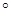 ,求出
,求出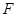 点坐标,从而可得到
点坐标,从而可得到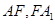 的长度,则易求出其比值.
的长度,则易求出其比值.
试题解析:
如图,以点 为原点建立空间直角坐标系,依题意得
为原点建立空间直角坐标系,依题意得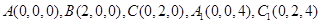 ,⑴因为
,⑴因为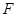 为中点,则
为中点,则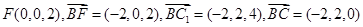 ,
,
设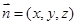 是平面
是平面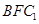 的一个法向量,则
的一个法向量,则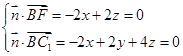 ,得
,得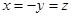 ,取
,取 ,则
,则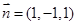 ,设直线
,设直线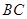 与平面
与平面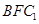 的法向量
的法向量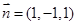 的夹角为
的夹角为 ,则
,则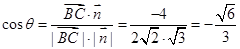 ,所以直线
,所以直线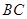 与平面
与平面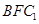 所成角的正弦值为
所成角的正弦值为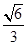 ;
;
⑵设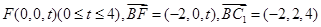 ,设
,设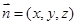 是平面
是平面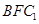 的一个法向量,则
的一个法向量,则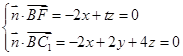 ,取
,取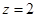 ,则
,则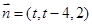 ,
,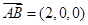 是平面
是平面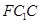 的一个法向量,
的一个法向量,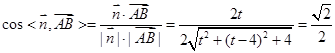 ,得
,得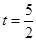 ,即
,即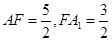 ,所以当
,所以当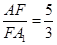 时,二面角
时,二面角 的大小是
的大小是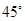 .
.
考点:运用空间向量解决线面角与面面角问题,要掌握线面角与面面角的公式,要注意合理建系.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
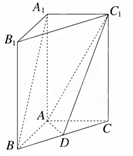
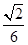 ,求线段AM的长.
,求线段AM的长.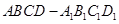 的所有棱长都相等,
的所有棱长都相等,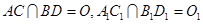 ,四边形
,四边形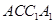 和四边形
和四边形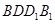 为矩形.
为矩形. 底面
底面 ;
;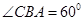 ,求二面角
,求二面角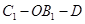 的余弦值.
的余弦值.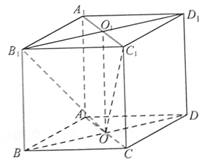
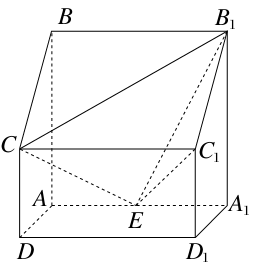
 的底面
的底面 是等腰直角三角形,
是等腰直角三角形, ,侧棱
,侧棱 底面
底面 ,
, 是
是 的中点,
的中点, 是
是 上的点.
上的点. 与
与 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示); ,求线段
,求线段 的长.
的长.
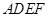 与梯形
与梯形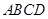 所在的平面互相垂直,
所在的平面互相垂直,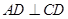 ,
, ∥
∥ ,
,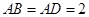 ,
,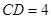 ,
,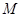 为
为 的中点.
的中点.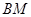 ∥平面
∥平面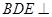 平面
平面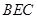 ;
;
 为平行四边形,
为平行四边形,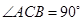 ,
,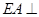 平面
平面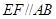 ,
,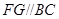 ,
,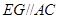 ,
,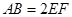 .
.
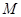 是线段
是线段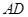 的中点,求证:
的中点,求证: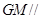 平面
平面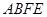 ;
;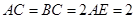 ,求二面角
,求二面角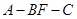 的余弦值.
的余弦值. 关于xOy面的对称点,则
关于xOy面的对称点,则 =
=  ,
, (
( 两两互相垂直的单位向量),那么
两两互相垂直的单位向量),那么 = .
= .