题目内容
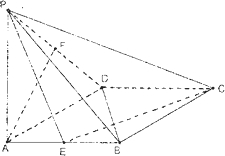 如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点.
如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点.(1)求证:PC⊥BD;
(2)求证:AF∥平面PEC;
(3)在线段BC上是否存在一点M,使AF⊥平面PDM?
若存在,指出点M的位置;若不存在,说明理由.
分析:(1)先构造线面垂直,然后利用线面垂直的定义,可得线线垂直.
(2)要证线面平行先证线线平行:取PC的中点K,连接FK、EK,则四边形AEKF是平行四边形,得到AF∥EK,然后利用线面平行的判定定理即得AF∥平面PEC.
(3)由于菱形ABCD中,∠DAB=60°,所以△BCD为正三角形,取CB的中点M,则DM⊥BC,然后利用底面中的平行关系,可得线线垂直,从而得到线面垂直.
(2)要证线面平行先证线线平行:取PC的中点K,连接FK、EK,则四边形AEKF是平行四边形,得到AF∥EK,然后利用线面平行的判定定理即得AF∥平面PEC.
(3)由于菱形ABCD中,∠DAB=60°,所以△BCD为正三角形,取CB的中点M,则DM⊥BC,然后利用底面中的平行关系,可得线线垂直,从而得到线面垂直.
解答:证明:(1)连接AC,则AC⊥BD.
∵PA⊥平面ABCD∴PA⊥BD又AC与PA相交于A
∴BD⊥平面PAC∴PC⊥BD(4分)
(2)取PC的中点K,连接FK、EK,
则四边形AEKF是平行四边形.
∴AF∥EK,又EK?平面PEC,AF?平面PEC,
∴AF∥平面PEC.(8分)
(3)当M是BC的中点时,可使AF⊥平面PDM,证明如下:(9分)
∵PA=DA,F是PD的中点∴AF⊥PD(10分)
∵菱形ABCD中,∠DAB=60°∴正△BCD中DM⊥BC
又AD∥BC∴DM⊥AD(12分)
∵PA⊥底面ABCD∴PA⊥DM∴DM⊥平面PAD
∴DM⊥AF又PD∩DM=D∴AF⊥平面PDM(14分)
∵PA⊥平面ABCD∴PA⊥BD又AC与PA相交于A
∴BD⊥平面PAC∴PC⊥BD(4分)
(2)取PC的中点K,连接FK、EK,
则四边形AEKF是平行四边形.
∴AF∥EK,又EK?平面PEC,AF?平面PEC,
∴AF∥平面PEC.(8分)
(3)当M是BC的中点时,可使AF⊥平面PDM,证明如下:(9分)
∵PA=DA,F是PD的中点∴AF⊥PD(10分)
∵菱形ABCD中,∠DAB=60°∴正△BCD中DM⊥BC
又AD∥BC∴DM⊥AD(12分)
∵PA⊥底面ABCD∴PA⊥DM∴DM⊥平面PAD
∴DM⊥AF又PD∩DM=D∴AF⊥平面PDM(14分)
点评:本题考查查了线面平行,线面垂直的判定和性质,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力,是个难题.

练习册系列答案
相关题目
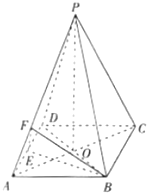 如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.
如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF. 如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.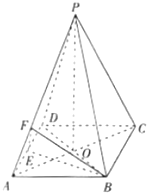 如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.
如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.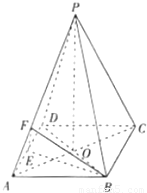
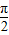 ),则四棱锥P-ABCD的体积V的取值范围是( )
),则四棱锥P-ABCD的体积V的取值范围是( )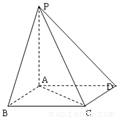
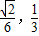 )
)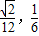 ]
] ]
] )
)