题目内容
已知圆x2+y2=4关于直线l对称的圆的方程为(x+3)2+(y-3)2=4,则直线l的方程为
- A.y=x+2
- B.y=x+3
- C.y=-x+3
- D.y=-x-3
B
分析:先求出两圆的圆心坐标,再求出两圆圆心连线构成的线段的垂直平分线方程,即为所求.
解答:由题意可得直线l是圆x2+y2=4和圆(x+3)2+(y-3)2=4两圆的圆心的垂直平分线,
两圆的圆心分别为O(0,0)、A(-3,3),线段OA的中点 C( ,
, ),
),
OA的斜率为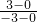 =-1,故直线l的斜率为1,
=-1,故直线l的斜率为1,
由点斜式求得直线l的方程为y- =1×(x+
=1×(x+ ),即y=x+3,
),即y=x+3,
故选B.
点评:本题主要考查求两个圆关于直线对称的性质,应用对称直线是两圆圆心连线构成的线段的垂直平分线,属于中档题.
分析:先求出两圆的圆心坐标,再求出两圆圆心连线构成的线段的垂直平分线方程,即为所求.
解答:由题意可得直线l是圆x2+y2=4和圆(x+3)2+(y-3)2=4两圆的圆心的垂直平分线,
两圆的圆心分别为O(0,0)、A(-3,3),线段OA的中点 C(
 ,
, ),
),OA的斜率为
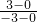 =-1,故直线l的斜率为1,
=-1,故直线l的斜率为1,由点斜式求得直线l的方程为y-
 =1×(x+
=1×(x+ ),即y=x+3,
),即y=x+3,故选B.
点评:本题主要考查求两个圆关于直线对称的性质,应用对称直线是两圆圆心连线构成的线段的垂直平分线,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目