题目内容
若非零向量 满足
满足 ,
, ,则
,则 与
与 的夹角为 .
的夹角为 .
【答案】分析:根据两个向量的数量积的定义,结合题中的条件可得cosθ= ,由此求出θ 的值.
,由此求出θ 的值.
解答:解:设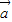 与
与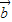 的夹角为θ,由题意可得
的夹角为θ,由题意可得 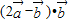 =2
=2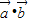 -
-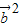 =2|
=2|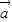 |•|
|•|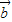 |cosθ-
|cosθ-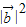 =0,
=0,
再由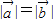 ,可得cosθ=
,可得cosθ= ,∴θ=60°,
,∴θ=60°,
故答案为:60°.
点评:本题考查两个向量的数量积的定义,根据三角函数的值求角的大小,求得cosθ= ,是解题的关键.
,是解题的关键.
 ,由此求出θ 的值.
,由此求出θ 的值.解答:解:设
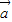 与
与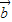 的夹角为θ,由题意可得
的夹角为θ,由题意可得 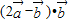 =2
=2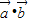 -
-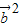 =2|
=2|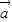 |•|
|•|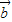 |cosθ-
|cosθ-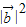 =0,
=0,再由
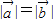 ,可得cosθ=
,可得cosθ= ,∴θ=60°,
,∴θ=60°,故答案为:60°.
点评:本题考查两个向量的数量积的定义,根据三角函数的值求角的大小,求得cosθ=
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
 满足
满足 、
、 |,则
|,则 满足
满足 ,
, ,则
,则 的夹角为 ( )
的夹角为 ( ) B.
B. C.
C. D.
D.
 满足
满足 ,
, ,则
,则 的夹角为( )
的夹角为( ) 满足
满足 ,
,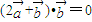 ,则
,则 的夹角为( )
的夹角为( )