题目内容
在一个不透明的盒子中,放有标号分别为1,2,3的三个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为x、y,记ξ=|x-2|+|x-y|.(1)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率;
(2)求随机变量ξ的分布列和数学期望.
分析:(1)由题意得到x、y可能的取值为1、2、3,根据x和y的值得到∴|x-2|和|y-x|的范围,从而得到随机变量ξ的最大值,求出最大值的概率.
(2)ξ的所有取值为0,1,2,3.ξ=0时,只有x=2,y=2这一种情况,ξ=2时,有x=1,y=2或x=3,y=2两种情况,ξ=3时,有x=3,y=1或x=1,y=3两种情况,而变量取1时,用其他几个变量的概率求得.
(2)ξ的所有取值为0,1,2,3.ξ=0时,只有x=2,y=2这一种情况,ξ=2时,有x=1,y=2或x=3,y=2两种情况,ξ=3时,有x=3,y=1或x=1,y=3两种情况,而变量取1时,用其他几个变量的概率求得.
解答:解:(1)∵x、y可能的取值为1、2、3,
∴|x-2|≤1,|y-x|≤2
∴ξ≤3,且当x=3,y=1或x=1,y=3时,ξ=3
因此随机变量ξ的最大值为3.
∵有放回地抽两张卡片的所有情况有3×3=9种,
∴P(ξ=3)=
∴随机变量ξ的最大值为3,事件“ξ取得最大值”的概率为
.
(2)ξ的所有取值为0,1,2,3.
∵ξ=0时,只有x=2,y=2这一种情况,
ξ=2时,有x=1,y=2或x=3,y=2两种情况,
ξ=3时,有x=3,y=1或x=1,y=3两种情况,
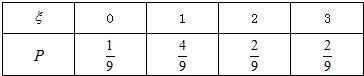
∴P(ξ=0)=
,P(ξ=2)=
,P(ξ=3)=
,P(ξ=1)=1-
-
-
=
则随机变量ξ的分布列为:
∴数学期望Eξ=0×
+1×
+2×
+3×
=
.
∴|x-2|≤1,|y-x|≤2
∴ξ≤3,且当x=3,y=1或x=1,y=3时,ξ=3
因此随机变量ξ的最大值为3.
∵有放回地抽两张卡片的所有情况有3×3=9种,
∴P(ξ=3)=
| 2 |
| 9 |
∴随机变量ξ的最大值为3,事件“ξ取得最大值”的概率为
| 2 |
| 9 |
(2)ξ的所有取值为0,1,2,3.
∵ξ=0时,只有x=2,y=2这一种情况,
ξ=2时,有x=1,y=2或x=3,y=2两种情况,
ξ=3时,有x=3,y=1或x=1,y=3两种情况,
∴P(ξ=0)=
| 1 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 1 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 4 |
| 9 |
则随机变量ξ的分布列为:

∴数学期望Eξ=0×
| 1 |
| 9 |
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 14 |
| 9 |
点评:本题应用分类讨论思想对于题目中出现的变量进行讨论,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
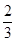 ,则
,则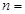 __________
__________  ,记
,记 .
. 的最大值,并求事件“
的最大值,并求事件“