题目内容
17.已知f(x)=$\frac{1}{3}{x^3}+m{x^2}$-2x,x∈R.(1)若m=-$\frac{1}{2}$,求f(x)的极值.
(2)若f(x)对于任意的x1,x2∈[-1,1]恒有(x1-x2)(f(x1)-f(x2))<0,求实数m的取值范围.
分析 (1)将m=-$\frac{1}{2}$代入函数的表达式,求出函数f(x)的导数,得到函数的单调区间,从而求出函数的极值;
(2)问题转化为x2+2mx-2≤0在[-1,1]恒成立,通过讨论x的范围,结合函数的单调性,从而求出m的范围.
解答 解:(1)m=-$\frac{1}{2}$时,f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2-2x,
∴f′(x)=x2-x-2=(x-2)(x+1),
令f′(x)>0,解得:x>2或x<-1,
令f′(x)<0,解得:-1<x<2,
∴函数f(x)在(-∞,-1),(2,+∞)递增,在(-1,2)递减,
∴x=2时,函数取得极小值$-\frac{10}{3}$;x=-1时,函数取得极大值$\frac{7}{6}$;
(2)f′(x)=x2+2mx-2,
若f(x)对于任意的x1,x2∈[-1,1]恒有(x1-x2)(f(x1)-f(x2))<0,
则函数f(x)在[-1,1]上递减,即f′(x)≤0在[-1,1]恒成立,
即x2+2mx-2≤0在[-1,1]恒成立,(*),
①x=0时,-2≤0,成立,
②-1≤x<0时,(*)可化为:m≥$\frac{{-x}^{2}+2}{2x}$,
设g(x)=$\frac{-{2x}^{2}+2}{2x}$=-$\frac{x}{2}$+$\frac{2}{x}$,
则g′(x)=-$\frac{1}{2}$-$\frac{2}{{x}^{2}}$<0,g(x)在[-1,0)递减,
∴g(x)max=g(-1)=-$\frac{1}{2}$,
∴m≥-$\frac{1}{2}$,
③0x≤1时,(*)可化为:m≤$\frac{{-x}^{2}+2}{2x}$,
设g(x)=$\frac{-{2x}^{2}+2}{2x}$=-$\frac{x}{2}$+$\frac{2}{x}$,
则g′(x)=-$\frac{1}{2}$-$\frac{2}{{x}^{2}}$<0,g(x)在(0,1]递减,
∴g(x)min=g(1)=$\frac{1}{2}$,
∴m≤$\frac{1}{2}$,
综上:$-\frac{1}{2}≤m≤\frac{1}{2}$.
点评 本题考查了函数的单调性,函数的极值问题,函数恒成立问题,考查导数的应用,是一道中档题.

| A. | [0,π] | B. | [0,$\sqrt{2}$π] | C. | [0,$\sqrt{3}π$] | D. | [0,2π] |
| A. | 能确定一个平面或不能确定平面 | B. | 可以确定一个平面 | ||
| C. | 能确定无数个平面 | D. | 能确定一个或无数个平面 |
| A. | 从6名同学中,选出4名参加数学竞赛,每个人被选中的可能性大小 | |
| B. | 同时掷两枚骰子,点数和为7的概率 | |
| C. | 近三天中有一天降雪的概率 | |
| D. | 10个人站成一排,其中甲,乙相邻的概率 |
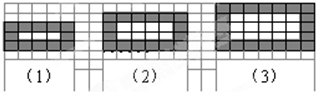 如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.
如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.