题目内容
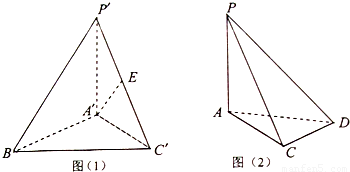
如图(1),三棱锥P′-A′BC′中,P′A′⊥平面A′BC′,△A′BC′是正三角形,E是P′C′的中点:如图(2),三棱锥P-ACD中,PA⊥平面ACD,∠ACD=90°,∠DAC=30°,若△P′A′C′≌△PAC,现将两个三棱锥拼接成四棱锥P-ABCD,使得面P′A′C′与面PAC完全重合,在四棱锥P-ABCD中,解答以下问题:
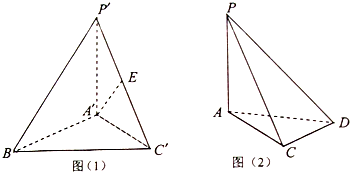
(I)求证:CD⊥AE;
(Ⅱ)当PA=AC=
时,求棱锥E-ABCD的体积.

(I)求证:CD⊥AE;
(Ⅱ)当PA=AC=
| 3 |
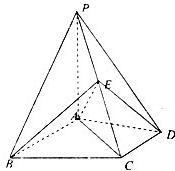
(I)证明:如图,由于P′A′⊥平面A′BC′,PA⊥平面ACD,∴A,B,C,D四点共面
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD
∵AC⊥CD,PA∩AC=A
∴CD⊥平面PAC,
∵E是PC的中点,∴CD⊥AE
(II)∵E是PC的中点,
∴点E到平面ABCD的距离等于点P到平面ABCD的距离的一半
∴VE-ABCD=
| 1 |
| 2 |
∴SABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
∴VE-ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
5
| ||
| 4 |
| 3 |
| 5 |
| 8 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
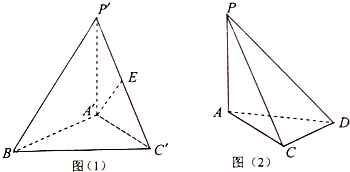
 如图(1),三棱锥P′-A′BC′中,P′A′⊥平面A′BC′,△A′BC′是正三角形,E是P′C′的中点;如图(2),PA⊥平面ACD,∠ACD=90°,∠DAC=30°.若△P′A′C′≌△PAC,现将两个三棱锥拼接成四棱锥P-ABCD,使得面△P′A′C′与面PAC完全重合.解答下列问题:
如图(1),三棱锥P′-A′BC′中,P′A′⊥平面A′BC′,△A′BC′是正三角形,E是P′C′的中点;如图(2),PA⊥平面ACD,∠ACD=90°,∠DAC=30°.若△P′A′C′≌△PAC,现将两个三棱锥拼接成四棱锥P-ABCD,使得面△P′A′C′与面PAC完全重合.解答下列问题: 如图(1),三棱锥P′-A′BC′中,P′A′⊥平面A′BC′,△A′BC′是正三角形,E是P′C′的中点;如图(2),PA⊥平面ACD,∠ACD=90°,∠DAC=30°.
如图(1),三棱锥P′-A′BC′中,P′A′⊥平面A′BC′,△A′BC′是正三角形,E是P′C′的中点;如图(2),PA⊥平面ACD,∠ACD=90°,∠DAC=30°.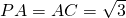 .
.
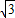 时,求棱锥E-ABCD的体积.
时,求棱锥E-ABCD的体积.