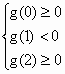题目内容
设函数
．
(1)求f(x)的单调区间；
(2)若当
时，不等式f(x)＜m恒成立，求实数m的取值范围；
(3)若关于x的方程
在区间[0，2]上恰好有两个相异的实根，求实数a的取值范围．
答案：
解析：
解析：
|
(1)函数的定义域为(－∞，－1)∪(－1，＋∞) ∵ 由于 由 ∴递增区间为(－2，－1)，(0，＋∞)；递减区间为(－∞，－2)，(－1，0)． (2)由 且 ∴ ∴ (3)方程 记 由 ∴g(x)在[0，1]上递减，在[1，2]上递增． 为使 ∴ ∴2－2ln2＜a≤3－2ln3． |
，
得－2＜x＜－1或x＞0，
得x＜－2或－1＜x＜0．
得x＝0或－2，由(1)知，f(x)在
上递减，在[0，e－1]上递增，又
，
，
，
时，
时，不等式f(x)＜m恒成立．
，即
．
，∴
．
得x＜－1或x＞1，由
得－1＜x＜1．
在[0，2]上恰好有两相异实根，只须g(x)＝0在[0，1)和(1，2]上各有实根．
练习册系列答案
导学全程练创优训练系列答案
相关题目
．
．
．
．
，求a的值．