题目内容
已知圆的参数方程
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线的极坐标方程为3ρcosα-4ρsinα-9=0,则直线与圆的位置关系是( )
|
| A、相切 | B、相离 |
| C、直线过圆心 | D、相交但直线不过圆心 |
分析:先利用sin2θ+cos2θ=1将圆的参数方程化成圆的普通方程,然后利用利用ρcosθ=x,ρsinθ=y,将直线的极坐标方程化成普通方程,最后计算圆心到直线的距离与半径进行比较即可判定位置关系.
解答:解:圆的参数方程
(θ为参数),
∴圆的普通方程为x2+y2=4
直线的极坐标方程为3ρcosα-4ρsinα-9=0,
∴直线的普通方程为3x-4y-9=0
而d=
<2
∴直线与圆的位置关系是相交但直线不过圆心
故选D.
|
∴圆的普通方程为x2+y2=4
直线的极坐标方程为3ρcosα-4ρsinα-9=0,
∴直线的普通方程为3x-4y-9=0
而d=
| 9 |
| 5 |
∴直线与圆的位置关系是相交但直线不过圆心
故选D.
点评:本小题主要考查圆的参数方程及直线与圆的位置关系的判断,以及转化与化归的思想方法,属于基础题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
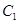 的参数方程为
的参数方程为 (
(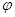 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆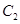 的极坐标方程为
的极坐标方程为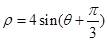 .
.