题目内容
过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为M1,设M1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2;…;依此下去,得到一系列点M1,M2,…Mn,…;设它们的横坐标a1,a2,…,
an…构成数列为{an}.
(Ⅰ)求数列{an}的通项公式;
( II)求证: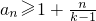 ;
;
( III)当k=2时,令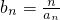 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
解:(Ⅰ)对y=xk求导数,
得y′=kxk-1,
点是Mn(an,ank)的切线方程是y-ank=kank-1(x-an).…(2分)
当n=1时,切线过点P(1,0),
即0-a1k=ka1k-1(1-a1),
得 ;
;
当n>1时,切线过点Pn-1(an-1,0),
即0-ank=kank-1(an-1-an),
得 .
.
所以数列{an}是首项 ,公比为
,公比为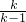 的等比数列,
的等比数列,
所以数列{an}的通项公式为 .…(4分)
.…(4分)
( II)应用二项式定理,得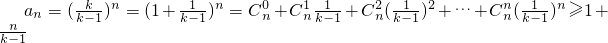 .…(8分)
.…(8分)
( III)当k=2时,an=2n,
数列{bn}的前n项和Sn= ,
,
同乘以 ,得
,得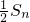 =
=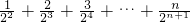 ,
,
两式相减,…(10分)
得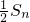 =
=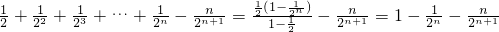 ,
,
所以Sn=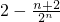 .…(12分)
.…(12分)
分析:(Ⅰ)对y=xk求导数,得y′=kxk-1,切点是Mn(an,ank)的切线方程是y-ank=kank-1(x-an).当n=1时, ;当n>1时,得
;当n>1时,得 .由此能求出数列{an}的通项公式.
.由此能求出数列{an}的通项公式.
( II)应用二项式定理,得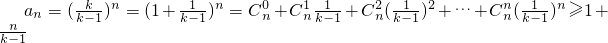 .
.
( III)当k=2时,an=2n,数列{bn}的前n项和Sn= ,利用错位相减法能够得到Sn=
,利用错位相减法能够得到Sn=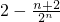 .
.
点评:本题考查数列的通项公式的求法,证明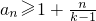 ,求数列的前n项和.对数学思维的要求比较高,要认真审题,注意错位相减法的灵活运用,本题有一定的探索性.综合性强,难度大,易出错.
,求数列的前n项和.对数学思维的要求比较高,要认真审题,注意错位相减法的灵活运用,本题有一定的探索性.综合性强,难度大,易出错.
得y′=kxk-1,
点是Mn(an,ank)的切线方程是y-ank=kank-1(x-an).…(2分)
当n=1时,切线过点P(1,0),
即0-a1k=ka1k-1(1-a1),
得
 ;
;当n>1时,切线过点Pn-1(an-1,0),
即0-ank=kank-1(an-1-an),
得
 .
.所以数列{an}是首项
 ,公比为
,公比为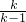 的等比数列,
的等比数列,所以数列{an}的通项公式为
 .…(4分)
.…(4分)( II)应用二项式定理,得
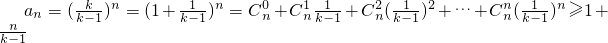 .…(8分)
.…(8分)( III)当k=2时,an=2n,
数列{bn}的前n项和Sn=
 ,
,同乘以
 ,得
,得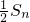 =
=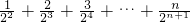 ,
,两式相减,…(10分)
得
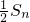 =
=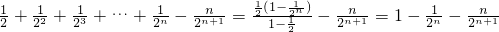 ,
,所以Sn=
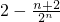 .…(12分)
.…(12分)分析:(Ⅰ)对y=xk求导数,得y′=kxk-1,切点是Mn(an,ank)的切线方程是y-ank=kank-1(x-an).当n=1时,
 ;当n>1时,得
;当n>1时,得 .由此能求出数列{an}的通项公式.
.由此能求出数列{an}的通项公式.( II)应用二项式定理,得
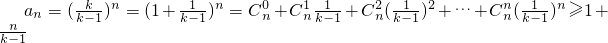 .
.( III)当k=2时,an=2n,数列{bn}的前n项和Sn=
 ,利用错位相减法能够得到Sn=
,利用错位相减法能够得到Sn=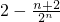 .
.点评:本题考查数列的通项公式的求法,证明
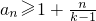 ,求数列的前n项和.对数学思维的要求比较高,要认真审题,注意错位相减法的灵活运用,本题有一定的探索性.综合性强,难度大,易出错.
,求数列的前n项和.对数学思维的要求比较高,要认真审题,注意错位相减法的灵活运用,本题有一定的探索性.综合性强,难度大,易出错. 
练习册系列答案
相关题目

 (2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.
(2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.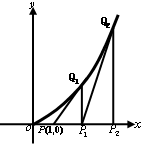 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.