题目内容
 已知函数y=|x|
已知函数y=|x|①判断该函数在(-4,0)上的单调性,并证明.
②画函数y=|x|在[-2,1]上的图象,并确定其最大值和最小值.
分析:①函数y=f(x)=|x|在(-4,0)上是减函数,用单调性定义可以证明结论是正确的;
②画出函数y=|x|在[-2,1]上的图象,由图象得出y=|x|在闭区间上的最值.
②画出函数y=|x|在[-2,1]上的图象,由图象得出y=|x|在闭区间上的最值.
解答:解:①函数y=f(x)=|x|在(-4,0)上是减函数,证明如下:
设x1,x2是区间(-4,0)上的任意两个值,且x1<x2,则x1<x2<0;
∴f(x1)-f(x2)=(-x1)-(-x2)=x2-x1>0;
∴f(x1)>f(x2),∴f(x)在(-4,0)上是减函数;
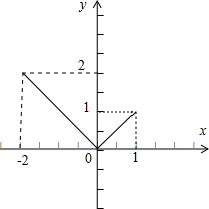
②函数y=|x|在[-2,1]上的图象如下,
 ;
;
由图象知:
函数y=|x|在[-2,1]上的最大值是2,最小值是0.
设x1,x2是区间(-4,0)上的任意两个值,且x1<x2,则x1<x2<0;
∴f(x1)-f(x2)=(-x1)-(-x2)=x2-x1>0;
∴f(x1)>f(x2),∴f(x)在(-4,0)上是减函数;
②函数y=|x|在[-2,1]上的图象如下,
 ;
;由图象知:
函数y=|x|在[-2,1]上的最大值是2,最小值是0.
点评:本题考查了函数单调性的证明与应用函数图象求函数在闭区间上的最值问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目