Question

已知数列{a_n}等差数列，{b_n}为等比数列，且满足：a₁₀₀₀+a₁₀₁₂=π，b₁b₁₄=-2，则=________．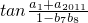

Answer 1

分析：等差数列{a_n}中，由性质a_m+a_n=a_p+a_q（其中m+n=p+q），得a₁+a₂₀₁₁=a₁₀₀₀+a₁₀₁₂，等比数列{b_n}中，由性质b_mb_n=b_pb_qm+n=p+q，得b₇b₈=b₁b₁₄，代入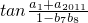计算可得．
解答：在等差数列{a_n}中，a₁+a₂₀₁₁=a₁₀₀₀+a₁₀₁₂=π，等比数列{b_n}中，b₇b₈=b₁b₁₄=-2，
∴===．
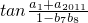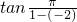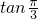故答案为：．
点评：本题考查了等差，等比数列性质的应用；在等差数列{a_n}中，有a_m+a_n=a_p+a_q，等比数列{b_n}中，有b_mb_n=b_pb_q（其中m+n=p+q），这两个公式在解题时应用很方便．