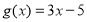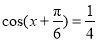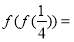题目内容
已知函数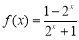 .
.
(1)判断函数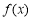 的奇偶性并证明;
的奇偶性并证明;
(2)当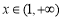 时,求函数
时,求函数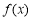 的值域.
的值域.
(1)奇函数,(2)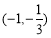 .
.
【解析】
试题分析:(1)判断函数奇偶性,从两个方面入手,一要判断定义域,若定义域不关于原点对称,则函数就为非奇非偶函数,二在函数定义域关于原点对称前提下,判断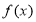 与
与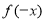 的关系,如只相等,则为偶函数,如只相反,则为奇函数,如既相等又相反,则既为奇函数又为偶函数,如既不相等又不相反,则为非奇非偶函数,本题定义域为R,研究
的关系,如只相等,则为偶函数,如只相反,则为奇函数,如既相等又相反,则既为奇函数又为偶函数,如既不相等又不相反,则为非奇非偶函数,本题定义域为R,研究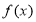 与
与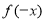 的关系时需将负指数化为对应正指数的倒数,(2)研究函数的值域,一要看函数解析式的结构,本题是可化为
的关系时需将负指数化为对应正指数的倒数,(2)研究函数的值域,一要看函数解析式的结构,本题是可化为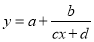 型,二是结合定义域利用函数单调性求值域.
型,二是结合定义域利用函数单调性求值域.
试题解析:(1)∵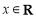 ,
,
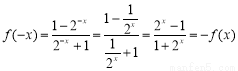 , 4分
, 4分
∴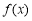 是奇函数. 5分
是奇函数. 5分
(2)令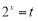 ,则
,则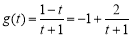 . 7分
. 7分
∵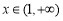 ,∴
,∴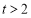 ,∴
,∴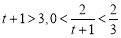 ,∴
,∴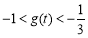 ,
,
所以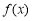 的值域是
的值域是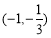 . 10分
. 10分
考点:函数奇偶性,函数值域.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目