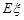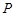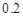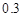题目内容
18、某运动员射击一次所得环数X的分布如下:

现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ
(Ⅰ)求该运动员两次都掵中7环的概率;
(Ⅱ)求ξ的分布列.
(Ⅲ)求ξ的数学希望

现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ
(Ⅰ)求该运动员两次都掵中7环的概率;
(Ⅱ)求ξ的分布列.
(Ⅲ)求ξ的数学希望
分析:(Ⅰ)由表示数据,我们可得运动员命中7环的概率为0.2,然后根据分步事件概率乘法公式,及求出该运动员两次都命中7环的概率.
(Ⅱ)由表中数据可得ξ的可能取值为7、8、9、10,然后分别讨论ξ取7、8、9、10时的情况及对应的概率,即可得到ξ的分布列.
(Ⅲ)将(2)中的ξ的分布列中数据,代入数学期望公式,即可求解.
(Ⅱ)由表中数据可得ξ的可能取值为7、8、9、10,然后分别讨论ξ取7、8、9、10时的情况及对应的概率,即可得到ξ的分布列.
(Ⅲ)将(2)中的ξ的分布列中数据,代入数学期望公式,即可求解.
解答:解:(Ⅰ)求该运动员两次都命中7环的概率为P(7)=0.2×0.2=0.04;
(Ⅱ)ξ的可能取值为7、8、9、10
P(ξ=7)=0.04P(ξ=8)=2×0.2×0.3+0.32=0.21
P(ξ=9)=2×0.2×0.3+2×0.3×0.3+0.32=0.39
P(ξ=10)2×0.2×0.2+2×0.3×0.2+2×0.3×0.2+0.22=0.36ξ分布列为
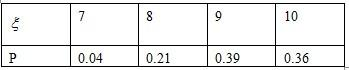
(Ⅲ)ξ的数学希望是Eξ=7×0.04+8×0.21+9×0.39+10×0.36=9.0719.
(Ⅱ)ξ的可能取值为7、8、9、10
P(ξ=7)=0.04P(ξ=8)=2×0.2×0.3+0.32=0.21
P(ξ=9)=2×0.2×0.3+2×0.3×0.3+0.32=0.39
P(ξ=10)2×0.2×0.2+2×0.3×0.2+2×0.3×0.2+0.22=0.36ξ分布列为

(Ⅲ)ξ的数学希望是Eξ=7×0.04+8×0.21+9×0.39+10×0.36=9.0719.
点评:本题考查的知识点是相互独立事件的概率乘法公式及离散型随机变量及其分布列、数学期望,相互独立事件的概率乘法公式用于解决分步问题的概率计算;分别讨论ξ取值,及取每一个值时的情况及对应的概率,是计算分布列的关键,分类讨论时,要注意不重不漏.

练习册系列答案
相关题目
(06年广东卷)(12分)
某运动员射击一次所得环数X的分布列如下:
X | 0-6 | 7 | 8 | 9 | 10 |
Y | 0 | 0.2 | 0.3 | 0.3 | 0.2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(Ⅰ)求该运动员两次都命中7环的概率;
(Ⅱ)求![]() 分布列;
分布列;
(Ⅲ) 求![]() 的数学期望.
的数学期望.
(10分)某运动员射击一次所得环数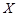 的分布如下:
的分布如下:
|
|
0~6 |
7 |
8 |
9 |
10 |
|
|
0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为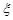 .
.
(I)求该运动员两次都命中7环的概率
(II)求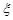 的分布列
的分布列
(III)求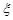 的数学期望
的数学期望