题目内容
以下命题①
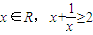 恒成立;
恒成立; ②△ABC中,若sinA=sinB,则A=B;
③若向量
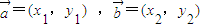 ,则
,则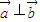 ?x1•x2+y1•y2=0;
?x1•x2+y1•y2=0;④对等差数列{an}前n项和Sn,若对任意正整数n有Sn+1>Sn,则an+1>an对任意正整数n恒成立;
⑤a=3是直线ax+2y+3a=0与直线3x+(a-1)y=a-7平行但不重合的充要条件.
其中正确的序号是 .
【答案】分析:对于①x<0时,不正确;对于②,因为△ABC中,当sinA=sinB时,A=B或A+B=π,故三角形是等腰三角形;对于③若向量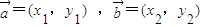 ,则
,则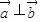 ?x1•x2+y1•y2=0,正确;对于④由Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故可得答案.
?x1•x2+y1•y2=0,正确;对于④由Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故可得答案.
解答:解:对于①因为当x<0时,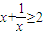 不成立,故不正确;对于②,因为△ABC中,当sinA=sinB时,A=B或A+B=π,故三角形是等腰三角形,故正确.对于③若向量
不成立,故不正确;对于②,因为△ABC中,当sinA=sinB时,A=B或A+B=π,故三角形是等腰三角形,故正确.对于③若向量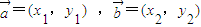 ,则
,则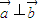 ?x1•x2+y1•y2=0,正确;
?x1•x2+y1•y2=0,正确;
对于④对等差数列{an}前n项和Sn,若对任意正整数n有Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故 a=3是直线ax+2y+3a=0与直线3x+(a-1)y=a-7平行且不重合的充要条件,故正确.
故答案为②③⑤.
点评:本题考查两直线平行的条件和性质,基本不等式,等差数列的性质以及由三角函数值判断角之间的关系.
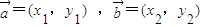 ,则
,则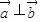 ?x1•x2+y1•y2=0,正确;对于④由Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故可得答案.
?x1•x2+y1•y2=0,正确;对于④由Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故可得答案.解答:解:对于①因为当x<0时,
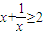 不成立,故不正确;对于②,因为△ABC中,当sinA=sinB时,A=B或A+B=π,故三角形是等腰三角形,故正确.对于③若向量
不成立,故不正确;对于②,因为△ABC中,当sinA=sinB时,A=B或A+B=π,故三角形是等腰三角形,故正确.对于③若向量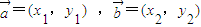 ,则
,则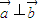 ?x1•x2+y1•y2=0,正确;
?x1•x2+y1•y2=0,正确;对于④对等差数列{an}前n项和Sn,若对任意正整数n有Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故 a=3是直线ax+2y+3a=0与直线3x+(a-1)y=a-7平行且不重合的充要条件,故正确.
故答案为②③⑤.
点评:本题考查两直线平行的条件和性质,基本不等式,等差数列的性质以及由三角函数值判断角之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
以下命题中正确的是( )
A、若x∈R且x≠0,则x+
| ||
| B、在△ABC中,若sin2A=sin2B,则△ABC是等腰三角形 | ||
| C、对等差数列{an}的前n项和Sn,若对任意正整数n都有Sn+1>Sn,则an+1>an对任意正整数n恒成立 | ||
| D、a=3是直线ax+2y+3a=0与直线3x+(a-1)y=a-7平行且不重合的充要条件 |