题目内容
已知函数 ,其中
,其中 且
且 .
.
(1)求证:函数 在点
在点 处的切线与
处的切线与 总有两个不同的公共点;
总有两个不同的公共点;
(2)若函数 在区间
在区间 上有且仅有一个极值点,求实数
上有且仅有一个极值点,求实数 的取值范围.
的取值范围.
(1)详见解析;(2)实数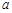 的取值范围是
的取值范围是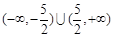 .
.
解析试题分析:(1)求证:函数 在点
在点 处的切线与
处的切线与 总有两个不同的公共点,先求出函数
总有两个不同的公共点,先求出函数 在点
在点 处的切线方程,因此对函数
处的切线方程,因此对函数 求导得
求导得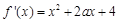 ,从而得
,从而得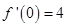 ,再求出
,再求出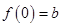 ,由点斜式即可得切线方程
,由点斜式即可得切线方程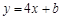 ,证切线与
,证切线与 总有两个不同的公共点,即方程
总有两个不同的公共点,即方程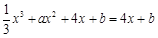 有两个不同的解,即
有两个不同的解,即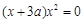 有两个不同的解,由已知
有两个不同的解,由已知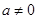 ,故方程存在两解,既得证.(2)若函数
,故方程存在两解,既得证.(2)若函数 在区间
在区间 上有且仅有一个极值点,只需
上有且仅有一个极值点,只需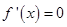 在区间
在区间 上有且仅有一个解,且在解的两边异号,而
上有且仅有一个解,且在解的两边异号,而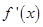 是二次函数,故只需
是二次函数,故只需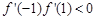 ,即可求出
,即可求出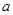 的取值范围.
的取值范围.
(1)由已知可得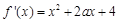 . 1分
. 1分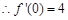 , 2分
, 2分
又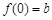 ,
,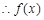 在
在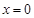 处的切线方程为
处的切线方程为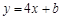 . 4分
. 4分
令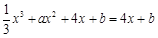 ,整理得
,整理得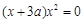 .
.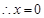 或
或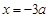 , 5分
, 5分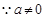
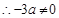 , 6分
, 6分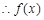 与切线有两个不同的公共点. 7分
与切线有两个不同的公共点. 7分
(2)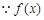 在
在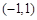 上有且仅有一个极值点,
上有且仅有一个极值点,
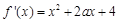 在
在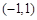 上有且仅有一个异号零点, 9分
上有且仅有一个异号零点, 9分
由二次函数图象性质可得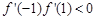 , 10分
, 10分
即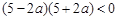 ,解得
,解得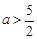 或
或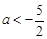 , 12分
, 12分
综上,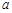 的取值范围是
的取值范围是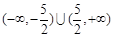 . 13分
. 13分
考点:导数的几何意义,函数的极值.

练习册系列答案
相关题目
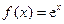 ,其中
,其中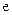 为自然对数的底数.
为自然对数的底数.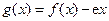 的单调区间;
的单调区间; 在点
在点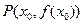 (其中
(其中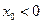 )处的切线为
)处的切线为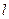 ,
,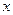 轴、
轴、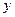 轴所围成的三角形面积为
轴所围成的三角形面积为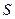 ,求
,求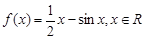 .
. 的递减区间;
的递减区间;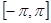 上的最值.
上的最值. 在
在 处的切线的斜率为
处的切线的斜率为 .
. 的值及函数
的值及函数 的最大值;
的最大值; .
. ,曲线
,曲线 经过点
经过点 ,
, 处的切线为
处的切线为 .
. 、
、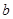 的值;
的值; ,使得
,使得 时,
时, 恒成立,求
恒成立,求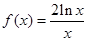
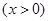
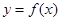 在
在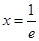 处的切线的斜率;
处的切线的斜率;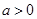 ,求函数
,求函数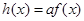 在
在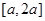 上的最大值.
上的最大值. ,
, .
. ,讨论
,讨论 在
在 内的单调性并求极值;
内的单调性并求极值; 时,恒有
时,恒有 .
.