题目内容
已知函数 (k为常数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(k为常数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(1)求k的值;
(2)求f(x)的单调区间;
(3)若g(x)=xexf(x)-2x-m在[1,+∞)恒有g(x)≥0,求实数m的取值范围.
解:(1)求导函数可得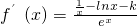
∵曲线y=f(x)在点(1,f(1))处的切线与x轴平行
∴f′(1)=0,
∴k=1;
(2)求导数得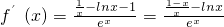 (x>0)
(x>0)
当x∈(0,1),f′(x)>0;当x>1,f′(x)<0,
∴f(x)的递增区间为(0,1),递减区间为(1,+∞);
(3)g(x)=xlnx-x-m≥0,∴m≤xlnx-x
令h(x)=xlnx-x,则h′(x)=lnx,∵x>1,h′(x)>0
∴h(x)min=h(1)=-1,
∴m≤-1
分析:(1)求导函数,利用曲线y=f(x)在点(1,f(1))处的切线与x轴平行,可得f′(1)=0,从而可求k的值;
(2)由导数的正负,可得函数的单调区间;
(3)分离参数,利用导数确定函数的最值,即可求得实数m的取值范围.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查恒成立问题,分离参数求函数的最值,是求恒成立问题的常用方法.
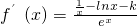
∵曲线y=f(x)在点(1,f(1))处的切线与x轴平行
∴f′(1)=0,
∴k=1;
(2)求导数得
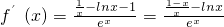 (x>0)
(x>0)当x∈(0,1),f′(x)>0;当x>1,f′(x)<0,
∴f(x)的递增区间为(0,1),递减区间为(1,+∞);
(3)g(x)=xlnx-x-m≥0,∴m≤xlnx-x
令h(x)=xlnx-x,则h′(x)=lnx,∵x>1,h′(x)>0
∴h(x)min=h(1)=-1,
∴m≤-1
分析:(1)求导函数,利用曲线y=f(x)在点(1,f(1))处的切线与x轴平行,可得f′(1)=0,从而可求k的值;
(2)由导数的正负,可得函数的单调区间;
(3)分离参数,利用导数确定函数的最值,即可求得实数m的取值范围.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查恒成立问题,分离参数求函数的最值,是求恒成立问题的常用方法.

练习册系列答案
相关题目




 (k为常数,e=2.71828……是自然对数的底数),曲线
(k为常数,e=2.71828……是自然对数的底数),曲线 在点
在点 处的切线与x轴平行。
处的切线与x轴平行。 的单调区间;
的单调区间; ,其中
,其中 为
为 ,
, 。
。 (a为常数),直线l与函数f(x)、g(x)的图象都相切,且l与函数f(x)的图象的切点的横坐标为1.
(a为常数),直线l与函数f(x)、g(x)的图象都相切,且l与函数f(x)的图象的切点的横坐标为1.