题目内容
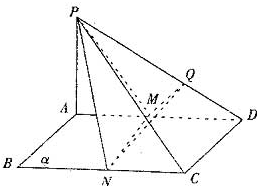如图，边长为2的正方形ABCD所在平面为α，PA⊥平面α，PA=2，M、N分别是AD、BC的中点，MQ⊥PD于Q．（1）求证平面PMN⊥平面PAD；
（2）二面角P-MN-Q的余弦值．
分析：（1）要证平面PMN⊥平面PAD，只需证MN⊥平面PAD即可；
（2）由（1）可知：MN⊥平面PAD，从而PMQ是二面角P-MN-Q的平面角，故可求．
（2）由（1）可知：MN⊥平面PAD，从而PMQ是二面角P-MN-Q的平面角，故可求．
解答：解：（1）正方体ABCD中，∵A、N分别是AD、BC的中点，∴MN⊥AD
又∵PA⊥平面α，MN?α，∴PA⊥MN，∴MN⊥平面PAD
又MN?平面PAD，平面PMN⊥平面PAD…（5分）
（2）由上可知：MN⊥平面PAD
∴PM⊥MN，QM⊥MN，∠PMQ是二面角P-MN-Q的平面角．…（8分）
PA=2，AD=2，则AM=1，PM=
PD=2
，MQ=
=
cos∠PMQ=
=
…（12分）
又∵PA⊥平面α，MN?α，∴PA⊥MN，∴MN⊥平面PAD
又MN?平面PAD，平面PMN⊥平面PAD…（5分）
（2）由上可知：MN⊥平面PAD
∴PM⊥MN，QM⊥MN，∠PMQ是二面角P-MN-Q的平面角．…（8分）
PA=2，AD=2，则AM=1，PM=
| 5 |
PD=2
| 2 |
| MD•PA |
| PD |
| ||
| 2 |
| MQ |
| PM |
| ||
| 10 |
点评：本题以线面垂直为载体，考查面面垂直，关键是寻找线面垂直，考查面面角，关键是得出表示面面角的平面角．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
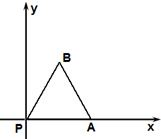如图放置的边长为1的正三角形PAB沿x轴滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系式是y=f（x），则f（x）在区间[-2，1]上的解析式是
（2011•洛阳一模）如图放置的边长为1的正三角形ABC沿x轴的正方向滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系是y=f（x）．则f（x）在两个相邻零点间的图象与x轴围成的面积是
如图所示，过正方形ABCD的中心O作OP⊥平面ABCD，已知正方形的边长为2，OP=2，连接AP、BP、CP、DP，M、N分别是AB、BC的中点，以O为原点，射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系．若E、F分别为PA、PB的中点，求A、B、C、D、E、F的坐标．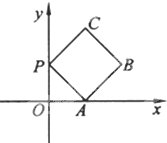
如图放置的边长为2的正方形PABC沿x轴滚动．设顶点P（x，y）的纵坐标与横坐标的函数关系是y=f（x），则f（x）的最小正周期为